Egenskaper ved Kjeglesnitt

Av Harald Pleym
www.hpleym.no

Figurene under er programmert og plottet med matematikk-programmet Maple

Lær deg Maple:
 www.hpleym.no/blikjent/blikjent.html
 www.hpleym.no/vgs/MatmVGS.html
 www.hpleym.no/MathWithMaple/index.html

Figurene under viser interessante egenskaper ved kjeglesnitt

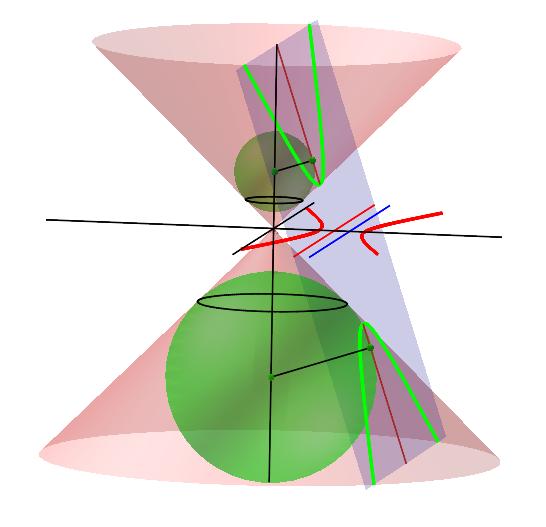
Den sirkulære tokappete kjeglen skjæres av det blå planet. Skjæringskurvene er en hyperbel. De to kulene tangerer kjeglen langs de sorte sirklene og tangerer planet i hyperbelens brennpunkter. Planet skjærer xy-planet langs den projiserte hyperbelens røde styrelinje.

Under er skjæringskurven mellom kjeglen og planet en parabel. Kulen under planet tangerer kjeglen langs den sorte sirkelen og planet i parabelens brennpunkt. Også her skjærer planet xy-planet langs den projiserte parabelens røde styrelinje.

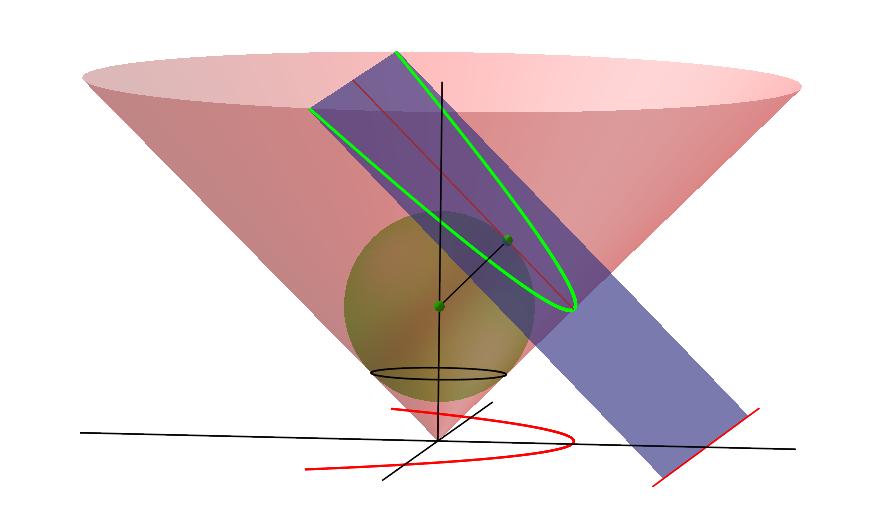
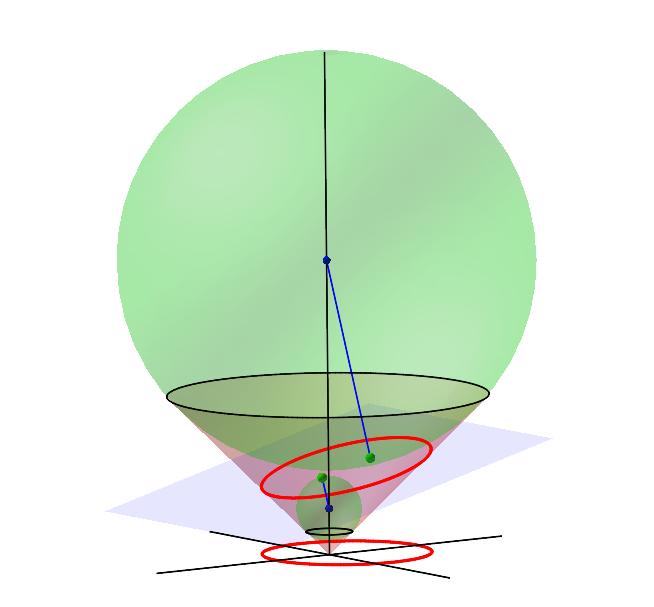
Neste figur visualiserer det såkalte "Ice-Cream-Cone-Proof".  Iskremtoppen, den store kulen, tangerer kjeglen langs den øverste sorte sirkelen og planet med ellipsen i ellipsens ene brennpunkt. Kula under planet tangerer kjeglen langs den underste sirkelen og planet med ellipsen i ellipsens andre brennpunkt. Ved en forlengelse av planet ville det skjære xy-planet langs den ene styrelinjen til ellipsen, som vist på figuren under iskrem-kjeglen.

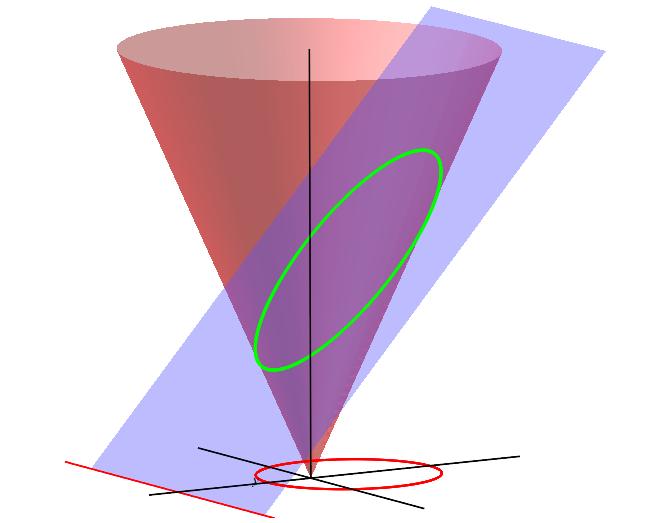
Her vises ellipsen i et skråere plan, og planet skjærer xy-planet langs den røde styrelinjen til den projiserte ellipsen.

Under ser vi både figuren over og speilbildet av figuren. Planenes skjæring med xy-planet går langs den projiserte ellipsens to styrelinjer.

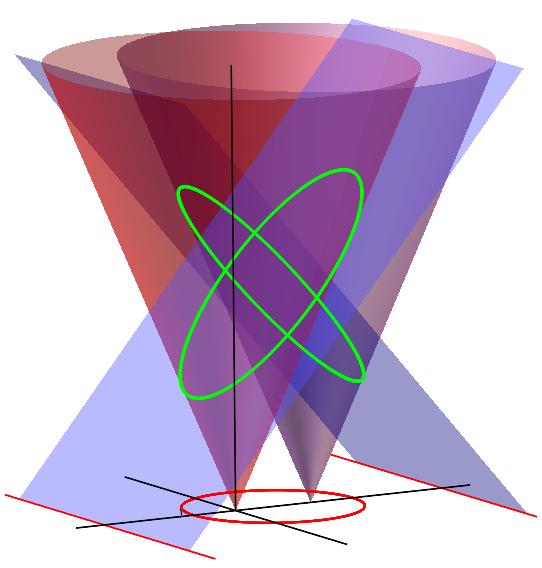
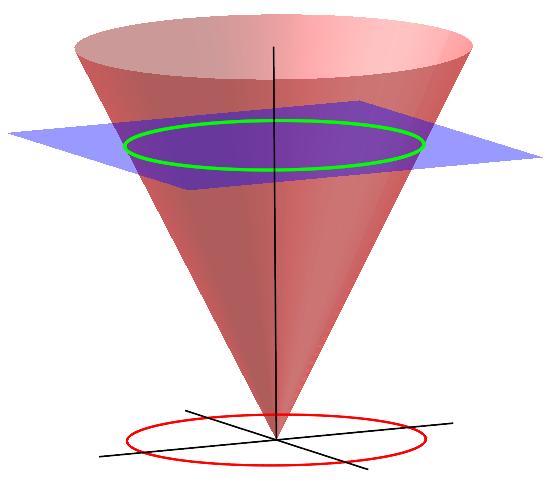
Skjæres den sirkulære kjeglen med et horisontalt plan blir skjæringskurven som kjent en sirkel.

Porsgrunn 11. desember 2019