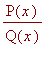 , where
, where
Educational use of Maple in Engineering
Mathematics
The Sixth Asian Technology Conference in Mathematics, ATCM
2002
RMIT University, Melbourne, Australia
December 2001
Harald Pleym
Telemark University College, Department of Technology
3914 Porsgrunn, Norway
Abstract
The main objective of this paper is to show how the computer algebra system Maple can be integrated as a valuable and powerful tool into the learning process of engineering mathematics. Maple can be used in several ways:
In this paper these methods of using Maple will be demonstrated with selected examples from calculus, differential equations, integral transforms and linear algebra. One of the beautiful qualities of Maple is that much can be done with relatively few commands and without involving formal programming with Maple. But when intermediate steps in solving a problem is clear, and especially if the focus is to demonstrate what happens to a solution when parameters are changed, it is often desirable and also an easy task to put the commands in question between "proc" and "end" to make a procedure. Examples of mixing steps together in this way will be shown.
Introduction
At Telemark College, Department of Technology in Porsgrunn, Norway, we have since 1995 incorporated the computer algebra system Maple as an integrated part of the learning process in egineering mathematics. I have developed interactive worksheets to present worked examples throughout all the subjects in the curriculum. They are designed to be used in conjunction with the textbook the students use in order to show how the computer algebra system Maple can be integrated as a valuable and powerful tool into the learning process of the material. These sample worksheets are also intended to be used as guides when the students prepare their own worksheets solutions to exercises and problems in mathematics or other homework where Maple is used. The main objective in this paper is therefore only to show a few examples on how Maple can be used both as an "instructor" and also to replace the use of pen and paper to present for instance a students homework as a live interactive Maple worksheet instead of a "dead" paper.
Integration by partials fractions
The first problem students often have before they can make use of the method of partial fractions is that they don't know how to find the factors of
![]() in the integrand of the form
in the integrand of the form
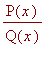 , where
, where
![]() and
and
![]() are polynomials in
are polynomials in
![]() and the degree of
and the degree of
![]() is less than the degree of
is less than the degree of
![]() . Secondly, they have to write down the integrand as a sum of simpler fractions corresponding to the factors of
. Secondly, they have to write down the integrand as a sum of simpler fractions corresponding to the factors of
![]() before they can find the constants by adding up the fractions in the decomposition, and then equating coefficients of like powers of
before they can find the constants by adding up the fractions in the decomposition, and then equating coefficients of like powers of
![]() in the numerator of the sum with those in
in the numerator of the sum with those in
![]() . Here the aim is to illustrate how we first can make direct use of Maple to find the factors and the sum of simpler fractions, before we proceed to present the method where all steps are shown. This is usually required in a student's homework solution. To illustrate how the decomposition is effected, we consider an integral where
. Here the aim is to illustrate how we first can make direct use of Maple to find the factors and the sum of simpler fractions, before we proceed to present the method where all steps are shown. This is usually required in a student's homework solution. To illustrate how the decomposition is effected, we consider an integral where
![]() can be written as a combination of linear factors and irreducible quadratic factors.
can be written as a combination of linear factors and irreducible quadratic factors.
Example 1
Find
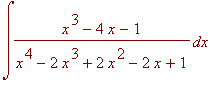 using partial fraction decomposition.
using partial fraction decomposition.
Solution
We define the integrand as the function
>
r:=x->(x^3-4*x-1)/(x^4-2*x^3+2*x^2-2*x+1):
R(x)=r(x);
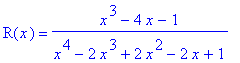
> factor(%);
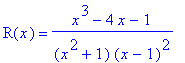
> Rf:=rhs(%):
The rational function
![]() may be decomposed into the sum of simple fractions of the type
may be decomposed into the sum of simple fractions of the type
> convert(%%,parfrac,x);
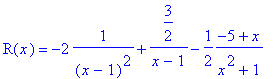
In the same way we could us Maple as an instructor to show us how the decomposition is effected when
![]() consists of
1)
linear factors, none of which are repeated,
2)
linear factors, all of which are the same,
3)
Irreducible quadratic factors, none of which are repeated,
4)
Irreducible quadratic factors, all of which are the same
.
consists of
1)
linear factors, none of which are repeated,
2)
linear factors, all of which are the same,
3)
Irreducible quadratic factors, none of which are repeated,
4)
Irreducible quadratic factors, all of which are the same
.
Now we decompose
![]() into the sum of the simple fractions of the type
into the sum of the simple fractions of the type
> eq:=Rf=A/(x-1)^2+B/(x-1)+(C*x+D)/(x^2+1):%;
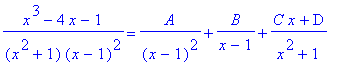
We simplify the right-hand side
> simplify(%);
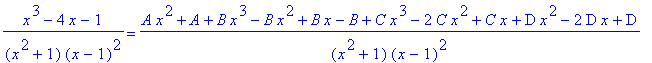
pick up the numerators
> map(numer,%);
![]()
and collect the coefficients of like powers .
> eqa:=collect(%,x):%;
![]()
Equating the coefficients of
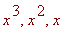 and the
constant term
on both sides gives
and the
constant term
on both sides gives
> seq(map(coeff,eqa,x,i),i=0..3):%;
![]()
Thus we have four equations in
![]() and
and
![]() , which may be solved to give
, which may be solved to give
> solve({%},{A,B,C,D});
![]()
Then we have
> subs(%,eq);
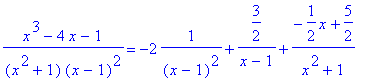
Now integration gives
> map(Int,%,x);
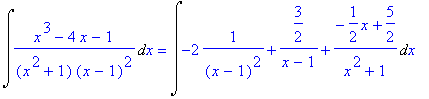
> lhs(%)=value(rhs(%))+C;
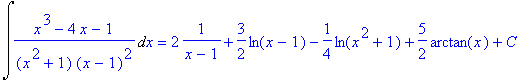
To check the result, we differentiate both sides
> diff(%,x);
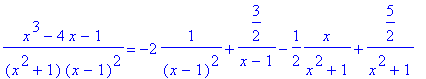
> simplify(%);
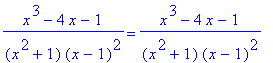
Newton's Method
Newton-Raphson's iterative method for generating a sequence
![]() , ...of approximations to a solution of
, ...of approximations to a solution of
![]() is given by the formula
is given by the formula
![x[n+1] = x[n]-f(x[n])/diff(f(x[n]),x)](images/Paper ATCM0135.gif)
The formula permits us to go from the
n
th approximation
![]() to the next approximation
to the next approximation
![]() . The formula is very easy to set up and apply repeatedly. When iterating for the root, it is often usual to present the calculation in tabular form. This can be done using the Maple spreadsheet, or calculate the values using a
for
-loop and present the result in a
sequence
of values or in an
array
. So, the goal here is to demonstrate that when the intermediate steps in solving the problem is understood, we put the individual commands between "
proc
" and "
end
" to make a procedure and make use of this to execute Newtons method on a routine basis.
. The formula is very easy to set up and apply repeatedly. When iterating for the root, it is often usual to present the calculation in tabular form. This can be done using the Maple spreadsheet, or calculate the values using a
for
-loop and present the result in a
sequence
of values or in an
array
. So, the goal here is to demonstrate that when the intermediate steps in solving the problem is understood, we put the individual commands between "
proc
" and "
end
" to make a procedure and make use of this to execute Newtons method on a routine basis.
Example 2
Find the root of
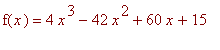 = 0
which lies between
= 0
which lies between
![]() and
and
![]() .
.
Solution
> f:=x->4*x^3-42*x^2+60*x+15: 'f(x)'=f(x);
![]()
We define Newtons formula
> N:=x->x-f(x)/D(f)(x);
![]()
Starting with
![]() , we get
, we get
> N(1.1); N(%); N(%); N(%);
![]()
![]()
![]()
![]()
If we use a for loop , we can represent the calculations as a sequence of values.
> x[0]:=1.1:
>
for n from 1 to 6 do
x[n]:=evalf(x[n-1]-f(x[n-1])/D(f)(x[n-1]));
od:
The sequence of values become
> S:=seq([n,x[n]],n=0..6):%;
![]()
![]()
We can also show the values in an array
> ['n','x[n]']; array([S]);
![]()
![matrix([[0, 1.1], [1, 3.085682327], [2, 2.117484062...](images/Paper ATCM0151.gif)
If we use Maple's spreadsheet , we can present the various steps in the calculations.
![-f(x[n])/Diff(f(x[n]),x)](images/Paper ATCM0156.gif)
|
||||
It is more convenient to make a small procedure for finding approximations by Newton's method on a routine basis , when the intermediate steps are known.
>
Newton:=proc(f,x0,N)
x[0]:=x0;
for n from 1 to N do
x[n]:=evalf(x[n-1]-f(x[n-1])/D(f)(x[n-1]));
od:
[seq(x[n],n=0..N)];
end:
> Newton(f,1.1,5);
![]()
To go from one approximation to the next approximation can be visualized by animation.
Animation
> with(calc):
> NewtonPlot(f,1.1,5,0.001,yellow);
![[Maple Plot]](images/Paper ATCM0199.gif)
First order linear differential equation - use of an integrating factor
Maple's dsolve command for solving differential equation, and in this context a first-order linear equation, usually gives us the answer promptly. But from an educational point of view it is important to use standard techniques and go through the solution process step by step as the textbooks do. When we use Maple, this step-by-step solution can be presented in a dynamic and interactive form. The following example shows this approach.
Example 3
a)
Find the particular solution of the
![]() circuit given by
circuit given by
![]()
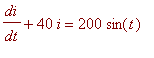 and satisfying the initial condition
and satisfying the initial condition
![]()
Solution
> restart:
> 20*diff(i(t),t)+40*i(t)=200*sin(t):%;
![]()
Division of both sides of the equation by
![]() gives
gives
> deq:=%/20:%;
![]()
Multiplication both sides by the integrating factor
> rho=exp(Int(2,t));
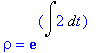
> value(%); rho:=rhs(%):
![]()
gives
> simplify(expand(deq*rho));
![]()
Here we see that the left-hand side of this equation may be written as the derivative of the product
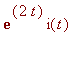 . Thus we have
. Thus we have
> eq:=Diff(rho*i(t),t)=rhs(%):%;
![]()
You should always check your work at this point by differentiating the left-hand side of the above equation.
> lhs(%)=value(lhs(%));
![]()
We integrate both sides of eq to obtain
> map(Int,eq,t);
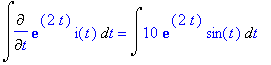
> map(int,eq,t)+(0=C);
![]()
> simplify(isolate(%,i(t))):%;
![]()
> eq1:=expand(%,power):%;
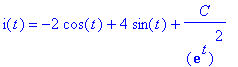
Substituting the initial conditions
> t=0,i(0)=0;
![]()
gives
> subs(%,eq1);
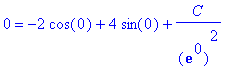
> isolate(%,C);
![]()
Then we have the particular solution
> subs(%,eq1);
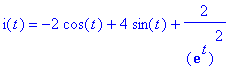
> lhs(%)=map(simplify,rhs(%),power);
![]()
It is recommended to check the answer.
> subs(%,lhs(deq)-rhs(deq)=0);
![]()
> %;
![]()
The Laplace transform
Laplace transforms are used frequently in the analysis and design of engineering systems. The usefulness of the transform is that a differential equation can be transformed into an algebraic equation which involves no derivatives at all. And so it reduces the problem of solving an initial value problem to the inspection of a table of transfoms. But without the use of a computer algebra system (CAS), the method is practically only if a sufficient large table of transforms is available. The use of Maple enable us if necessary to add our own functions to Laplace's internal lookup table by using the addtable function. And we are also freed from tedious manual partial fraction decomposition and other algebraic manipulations. The following step by step solution shows that Maple's Laplace transforms package is very useful for elegant and quick calculations of transforms, suitable for use in the classroom from a pedagogical point of view. It is convenient to start the solution process by defining the Laplace transform and the inverse Laplace transform by functions. The purpose of the alias facility is to allow us to state abbreviations for the longer names that Maple uses.
> with(inttrans):
> L:=f->laplace(f,t,s):invL:=F->invlaplace(F, s, t): alias(X(s)=L(x(t)),Y(s)=L(y(t)), F(s)=L(f(t))):
Example 4
Solve the system
2 x '' = -6 x + 2y
y
'' = 2
x
- 2
y
+
![]()
x (0) = 0, x '(0) = 0, y (0) = 0, y '(0) = 0
Solution
> sys:=2*diff(x(t),t,t)=-6*x(t)+2*y(t), diff(y(t),t,t)=2*x(t)-2*y(t)+4*sin(3*t):%;
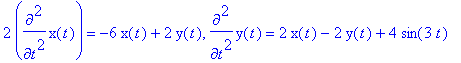
Initial conditions are
> inits:=x(0)=0,D(x)(0)=0,y(0)=0,D(y)(0)=0:%;
![]()
Laplace transformation gives
> L({sys});
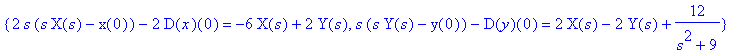
> subs(inits,%);
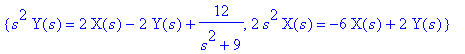
> solve(%,{X(s),Y(s)});
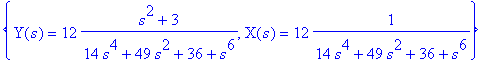
The partial fraction decomposition gives
> convert(%,parfrac,s);
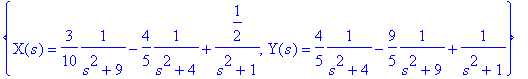
The inverse Laplace transform yields the solution
> invL(%);
![]()
We can also check this result by direct solution.
> dsolve({sys,inits},{x(t),y(t)},method=laplace);
![]()
Animation of the system
> with(calc):
> L1:=[[2,4],[1,2]]:init:=[0,0,0,0]: F1:=[0,4*sin(3*t),0]:
> SpringMassCouplet(L1,init,F1,22,60,p,scaling=unconstrained,axes=frame);
![[Maple Plot]](images/Paper ATCM01133.gif)
Eigenvalues and Eigenvectors
Eigenvalue problems are among the most important problems in connection with matrices and engineering applications, and they provide critical information in engineering design. The advantage of using Maple is that the method described in textbooks and used by instructors on the blackboard can be reproduced on the computer in the classroom. Eigenvalues are the roots of the characteristic equation
|
![]() I
-
A
| = 0
. Solving this equation is almost always easier said than done on a blackboard. And for large matrices we may not be able able to solve the characteristic equation exactly. And in this case a numerical approach may be the only possibility, which can be done interactively in the classroom using the power of Maple. The example here shows the sequences of calculations of eigenvalues and the corresponding eigenvectors using the "blackboard" method.
I
-
A
| = 0
. Solving this equation is almost always easier said than done on a blackboard. And for large matrices we may not be able able to solve the characteristic equation exactly. And in this case a numerical approach may be the only possibility, which can be done interactively in the classroom using the power of Maple. The example here shows the sequences of calculations of eigenvalues and the corresponding eigenvectors using the "blackboard" method.
Example 5
Find the eigenvalues and associated eigenvectors of the matrix
A
=
![matrix([[3, 0, 0], [-4, 6, 2], [16, -15, -5]])](images/Paper ATCM01135.gif) , and display the factorization
, and display the factorization
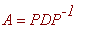
Solution
> with(linalg):
> A:=matrix(3,3,[3,0,0,-4,6,2,16,-15,-5]);
![A := matrix([[3, 0, 0], [-4, 6, 2], [16, -15, -5]])...](images/Paper ATCM01137.gif)
> 'det'(charmat(A,lambda))=charpoly(A,lambda);
![det(matrix([[lambda-3, 0, 0], [4, lambda-6, -2], [-...](images/Paper ATCM01138.gif)
The characteristic equation of A is
> rhs(%)=0;
![]()
> lambda:=solve(%,lambda);
![]()
With
![]() we get
we get
> Ac:=charmat(A,lambda[1]): X:=Vector([x,y,z]): b:=Vector([0,0,0]):
> evalm(Ac)*X=b;
![matrix([[-3, 0, 0], [4, -6, -2], [-16, 15, 5]])*_rt...](images/Paper ATCM01142.gif)
The augmented coefficient matrix of the system is
> augment(Ac,b);
![matrix([[-3, 0, 0, 0], [4, -6, -2, 0], [-16, 15, 5,...](images/Paper ATCM01143.gif)
Gauss-Jordan elimination with back substitution gives
> gaussjord(%);
![matrix([[1, 0, 0, 0], [0, 1, 1/3, 0], [0, 0, 0, 0]]...](images/Paper ATCM01144.gif)
> evalm(X)=backsub(%);
![]()
The eigenvector
> v[1]=subs(_t[1]=-3,convert(rhs(%),matrix));
![v[1] = matrix([[0], [1], [-3]])](images/Paper ATCM01146.gif)
is associated with
![]() to within a constant multiple. The eigenvectors for the remaining two eigenvalues can be produced in the same manner. Two show the
complete solution
, we use the
eigenvector command
.
to within a constant multiple. The eigenvectors for the remaining two eigenvalues can be produced in the same manner. Two show the
complete solution
, we use the
eigenvector command
.
> ev:=eigenvectors(A):%;
![]()
The matrix
![]() with the eigenvectors as columns is
with the eigenvectors as columns is
> P:=augment(seq(ev[i,3,1],i=1..3));
![P := matrix([[0, 0, 1], [1, 1, 0], [-3, -5/2, 2]])](images/Paper ATCM01150.gif)
> unprotect(D):
The diagonal entries of
![]() are eigenvalues of
are eigenvalues of
![]() .
.
> D:=diag(seq(ev[i,1],i=1..3));
![D := matrix([[0, 0, 0], [0, 1, 0], [0, 0, 3]])](images/Paper ATCM01153.gif)
> A=evalm(P)&*evalm(D)&*inverse(P);
![A = `&*`(`&*`(matrix([[0, 0, 1], [1, 1, 0], [-3, -5...](images/Paper ATCM01154.gif)
> evalm(%);
![matrix([[3, 0, 0], [-4, 6, 2], [16, -15, -5]]) = ma...](images/Paper ATCM01155.gif)
References
[1] C. H. Edwards and D. E. Penney. Calculus with Analytic Geometry, Prentice-Hall International, Inc ., 1998.
[2] C. H. Edwards and D. E. Penney. Differential Equations & Linear Algebra, Prentice-Hall International, Inc ., 2001.