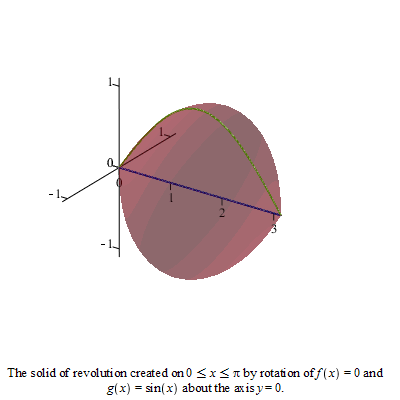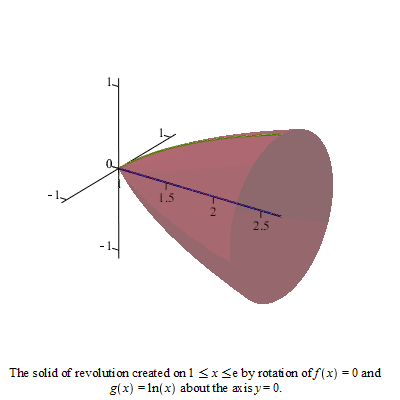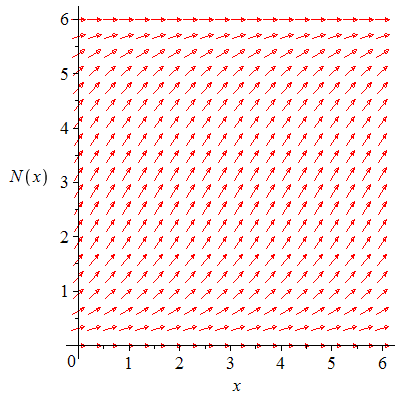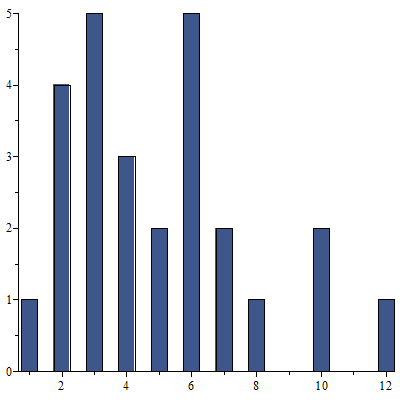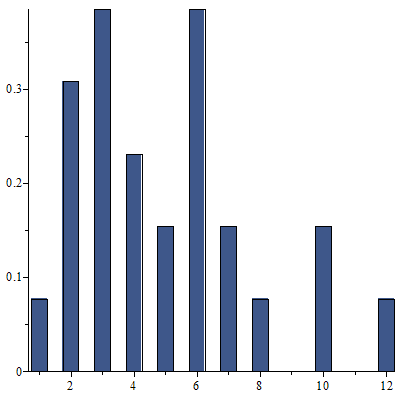Matematikk med Maple
for
videregående skole
© Harald Pleym
Dette er et lite utvalg av stoff som fins i e-boka Matematikk med Maple for videregående skole.
Vær oppmerksom på at denne konverteringen av Mapledokumenter til html-dokumenter (websider) medfører en betydelig forringelse av kvaliteten på dokumentene som er konvertert. Det gjelder både tekst, grafikk og plassering.
Det er spesielt iøynefallene at matematisk tekst (formler etc) ofte ikke
kommer på samme linje som den øvrige teksten etter konverteringen.
n-te røtter og potenser
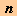 -te røtter -te røtter
|
Definisjon
|
Multiplikasjon
|
Divisjon
|
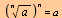
|
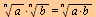
|
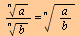
|
-
RasjonalNevner
 gjør nevneren i en brøk rasjonal
gjør nevneren i en brøk rasjonal
Eksempel 1
a) Regn ut 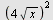
b) Skriv 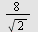 uten kvadratrot i nevneren. uten kvadratrot i nevneren.
Løsning
a)
| > |
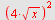 |
b)
| > |
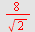 |
|
Her blir nevneren automatisk gjort rasjonal. Det skjer ikke med f.eks.
| > |
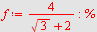 |
Med
RasjonalNevner
får vi
| > |
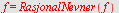 |
|
Logaritmeligninger
-
LøsLigning
og
solve
løser alle slike ligninger
-
combine
trekker sammen uttrykk
-
map
brukes for å anvende en funksjon på et utrykk
Eksempel 2
Løs ligningen
a) 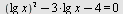
b) 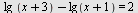
c) 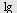 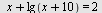
Løsning
a)
|
| > |
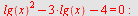 |
|
| > |
 |
|
b)
|
|
| > |
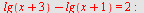 |
|
| > |
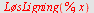 |
|
c)
|
|
| > |
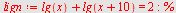 |
|
| > |
 |
|
| > |
 |
|
| > |
 |
|
| > |
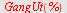 |
|
| > |
 |
| > |
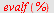 |
Her er det bare den positive roten som kan brukes.
|
Direkte løsning
| > |
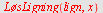 |
|
| > |
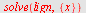 |
|
Ulikheter
Bruk av fortegnslinje er vanligvis et nyttig hjelpemiddel når man skal finne ut hvordan fortegnet til et uttrykk varierer med ulike verdier av variabelen 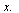 Men når man bruker et dataverktøy som Maple er bruk av fortegnslinjer helt unødvendig.
Men når man bruker et dataverktøy som Maple er bruk av fortegnslinjer helt unødvendig.
-
solve
eller
LøsLigning
løser også ulikheter
Eksempel 3
Løs ulikheten 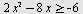
Løsning
|
| > |
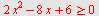 |
| > |
 |
| > |
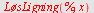 |
| > |
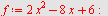 |
| > |
![`assign`(plt, plot(f, x = 0 .. 4, legend = f, tickmarks = [8, 8], gridlines)); -1](images/utvalg_56.gif)
![`assign`(plt, plot(f, x = 0 .. 4, legend = f, tickmarks = [8, 8], gridlines)); -1](images/utvalg_57.gif) |
|
| > |
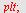 |
Vi ser at 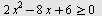 når når
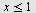 eller eller 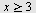
|
Eksempel 4
Løs ulikheten 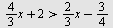
Løsning
|
| > |
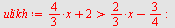 |
|
| > |
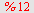 |
|
| > |
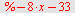 |
|
| > |
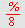 |
|
Med
LøsLigning
får vi svaret direkte.
|
| > |
 |
|
Vi kan også plotte uttrykkene på begge sider av ulikhetstegnet.
| > |
![`assign`(plt, plot([`+`(`*`(`+`(`*`(2, `*`(x))), `/`(1, 3)), 3), `+`(`*`(`+`(`*`(3, `*`(x))), `/`(1, 2)), `-`(`/`(1, 3)))], x = 0 .. 6, legend = [`+`(`*`(`+`(`*`(2, `*`(x))), `/`(1, 3)), 3), `+`(`*`(`...](images/utvalg_73.gif)
![`assign`(plt, plot([`+`(`*`(`+`(`*`(2, `*`(x))), `/`(1, 3)), 3), `+`(`*`(`+`(`*`(3, `*`(x))), `/`(1, 2)), `-`(`/`(1, 3)))], x = 0 .. 6, legend = [`+`(`*`(`+`(`*`(2, `*`(x))), `/`(1, 3)), 3), `+`(`*`(`...](images/utvalg_74.gif) |
|
| > |
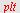 |
|
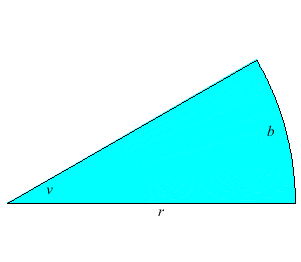
Radianer, grader og enhetssirkel
Radianer og grader
Det absolutte vinkelmålet  i radianer er forholdet mellom buen i radianer er forholdet mellom buen 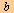 og radius og radius 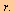
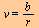
Overgang mellom grader og radianer er gitt ved
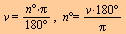
|
|
-
OmgjørEnhet
regner om fra grader til radianer eller omvendt
-
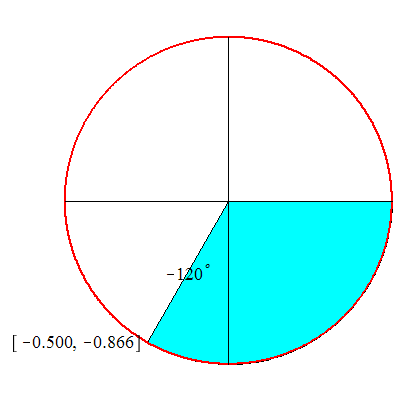
EnhetsSirkel
plotter vinkler på enhetssirkelen
Sinus, cosinus og tangens til vilkårlige vinkler
- Med
sin
,
cos
,
tan
og
cot
må vinkelen være i radianer
- Med
Sin
,
Cos
,
Tan
og
Cot
må vinkelen være i grader
De inverse funksjonene som gir vinkel i radianer som output er
-
sin
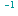 =
arcsin
,
cos
=
arcsin
,
cos
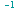 =
arcos
,
tan
=
arcos
,
tan
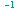 =
arctan
=
arctan
De inverse funksjonene som gir vinkel i grader som output er
Eksakte verdier
|
| > |
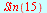 |
| > |
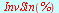 |
|
| > |
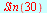 |
|
| > |
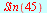 |
|
| > |
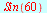 |
|
| > |
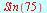 |
|
| > |
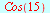 |
|
| > |
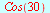 |
| > |
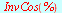 |
|
| > |
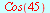 |
|
| > |
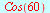 |
|
| > |
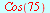 |
|
| > |
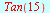 |
|
| > |
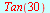 |
|
| > |
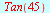 |
|
| > |
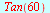 |
| > |
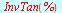 |
|
| > |
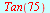 |
|
| > |
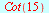 |
|
| > |
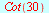 |
|
| > |
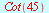 |
|
| > |
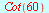 |
|
| > |
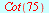 |
| > |
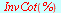 |
|
Cosinussetningen
Eksempel 5
I 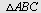 er er 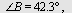 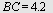 cm og cm og 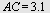 cm. Regn ut cm. Regn ut 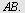
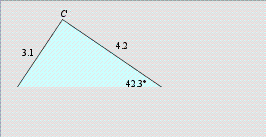
Løsning
Cosinussetningen gir
| > |
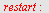 |
| > |
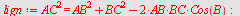 |
| > |
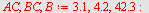 |
| > |
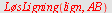 |
|
Det er altså to løsninger.
| > |
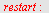 |
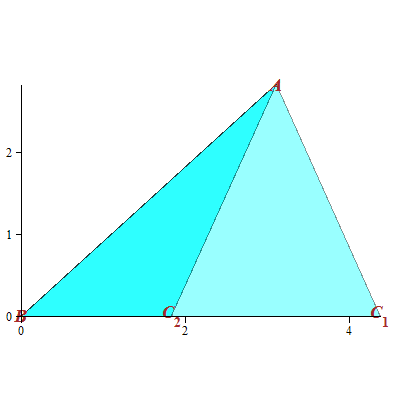
NB! Med kommandoen
Trekant
blir den oppgitte vinkelen, her 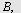 plassert i origo og bokstaveringen er mot urviseren. Da blir plassert i origo og bokstaveringen er mot urviseren. Da blir 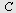 på figuren til venstre på figuren til venstre 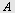 og og 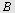 blir blir 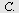
| > |
![Trekant([B = 42.3, c = 4.2, b = 3.1])](images/utvalg_164.gif) |
|
Høydesetningen i en trekant
-
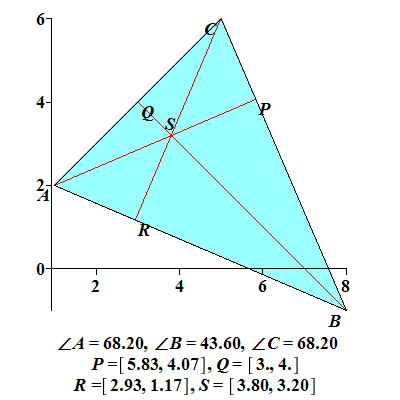
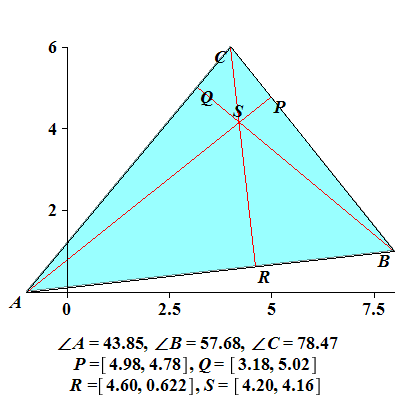
TrekantHøyder
plotter en trekant med høyder
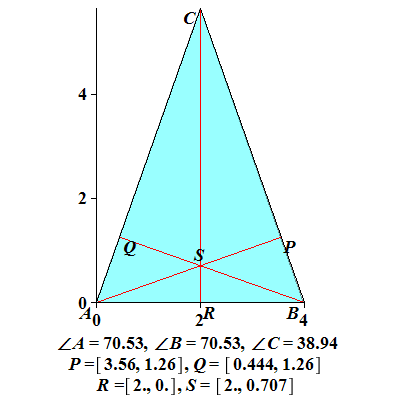
Eksempel 6
I 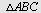 er er 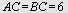 og og 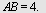 Høyden fra Høyden fra 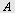 til til 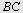 og høyden fra og høyden fra 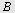 til til 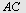 skjærer hverandre i skjærer hverandre i 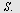 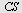 skjærer skjærer 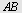 i i 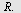 Beregn Beregn 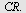
Løsning
Vi plasserer 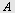 i origo og får følgende koordinater for i origo og får følgende koordinater for 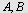 og og 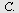
|
| > |
![`assign`(A, B, C, [0, 0], [4, 0], [2, sqrt(`+`(`^`(6, 2), `-`(`^`(2, 2))))]); -1](images/utvalg_194.gif) |
| > |
 |
|
| > |
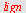 |
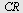 finnes av finnes av
| > |
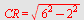 |
eller ved
| > |
![CR = Lengde(`+`(C, [-2, 0]))](images/utvalg_203.gif) |
| > |
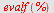 |
|
Sirkel, ellipse, hyperbel og parabel
-
Sirkel
plotter en sirkel, skriver opp ligningen for sirkelen på standard form og oppgir sirkelens radius, sentrum og areal
-
Ellipse
plotter en ellipse, skriver opp ligningen og oppgir sentrum, brennpunkter, store og lille akse, eksentrisitet og styrelinjer
-
Hyperbel
plotter en hyperbel, skriver opp ligningen og oppgir sentrum, brennpunkter, eksentrisitet, styrelinjer og asymptoter
-
Parabel
plotter en parabel, skriver opp ligningen og oppgir brennpunkt, toppunkt og styrelinje
-
FullstendigKvadrat
gjør om et kvadratisk uttrykk til et fullstendig kvadrat
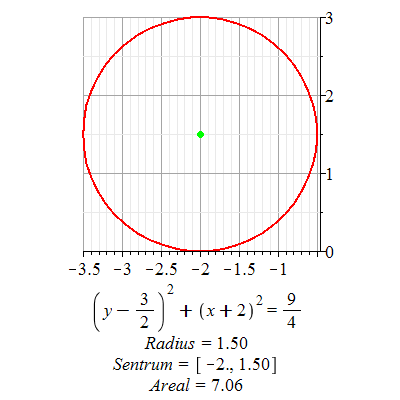
Eksempel 7
Finn sentrum og radius i sirkelen 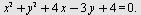 Plott sirkelen. Plott sirkelen.
Løsning
|
| > |
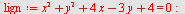 |
| > |
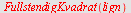 |
|
| > |
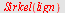 |
|
|
|
Eksempel 8
Hva fremstiller ligningen 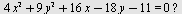
Løsning
|
| > |
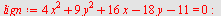 |
|
| > |
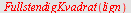 |
|
| > |
 |
|
| > |
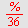 |
|
Ligningen fremstiller en ellipse med sentrum i 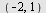 og store halvakse og store halvakse  og lille halvakse og lille halvakse 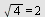
|
| > |
 |
|
Eksempel 9
Hva fremstiller ligningen 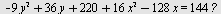
Løsning
|
| > |
![`assign`(lign[1], `+`(`-`(`*`(9, `*`(`^`(y, 2)))), `*`(36, `*`(y)), 220, `*`(16, `*`(`^`(x, 2))), `-`(`*`(128, `*`(x)))) = 144); -1](images/utvalg_227.gif) |
|
| > |
![FullstendigKvadrat(lign[1])](images/utvalg_228.gif) |
|
| > |
![`assign`(lign[2], `+`(`*`(`/`(1, 144), `*`(%)))); -1; %](images/utvalg_230.gif) |
|
| > |
![Hyperbel(lign[1])](images/utvalg_232.gif) |
|
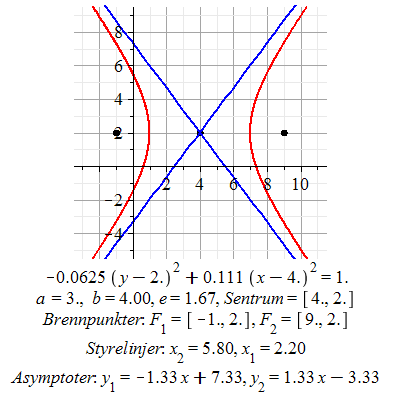
Ligningen fremstiller en hyperbel med sentrum i 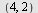 og reell akse paralell med og reell akse paralell med 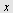 -aksen. -aksen. 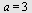 og og 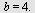
|
Asymptotene finnes ved å løse ligningen
| > |
![lhs(lign[2]) = 0](images/utvalg_238.gif) |
|
| > |
 |
|
| > |
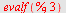 |
|
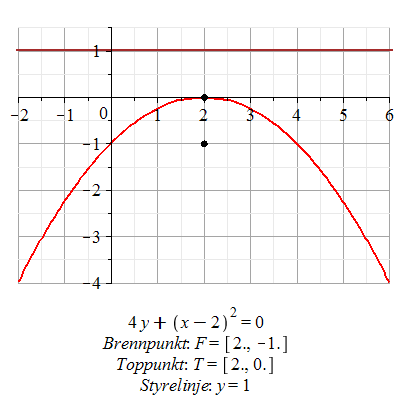
Eksempel 10
a) Hva fremstiller ligningen 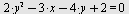 ? ?
b) 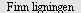 til parabelen med brennpunkt i til parabelen med brennpunkt i 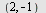 og styrelinje og styrelinje 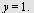
Løsning
|
a)
| > |
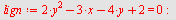 |
Ligningen fremstiller en parabel.
| > |
 |
|
b)
| > |
![Parabel(y = 1, [2, -1])](images/utvalg_251.gif) |
|
Vektorer
-
LagVektor
skriver ut en vektor med pilsymbol. Det samme fåes ved bruk av vektorpaletten
-
Vektor
plotter en vektor når tallstørrelser er oppgitt
-
PlottVektorSum
plotter en sum av vektorer
-
Lengde
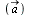 beregner
beregner 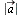
| > |
 |
|
| > |
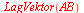 |
|
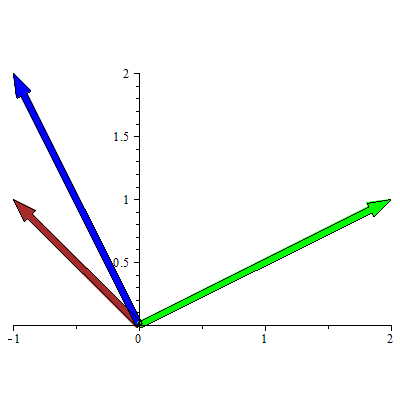
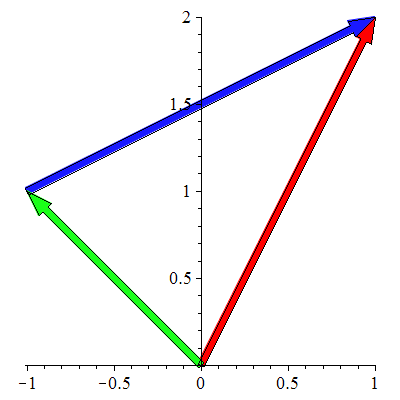
Eksempel 11
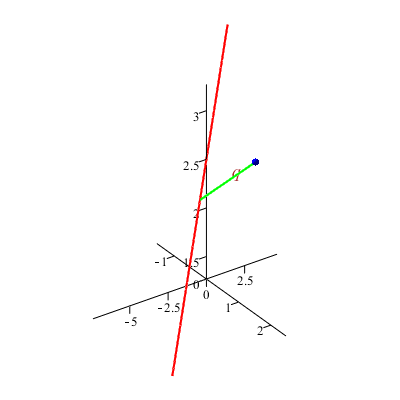
Plott vektorene 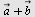 og og 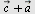 når når 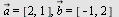 og og 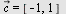
Løsning
|
| > |
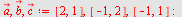 |
|
| > |
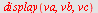 |
|
NB! Her velges fargene automatisk slik at fargene på vektorene vil kunne være annerledes enn de gitte. Resultantvektoren er alltid rød.
| > |
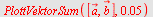 |
|
| > |
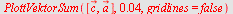 |
|
|
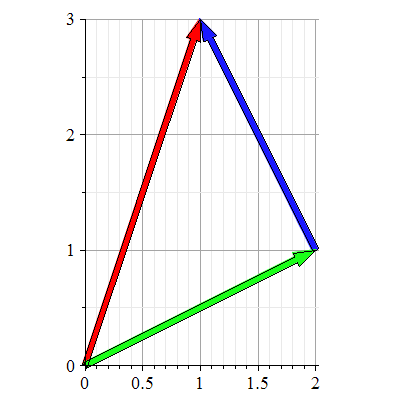
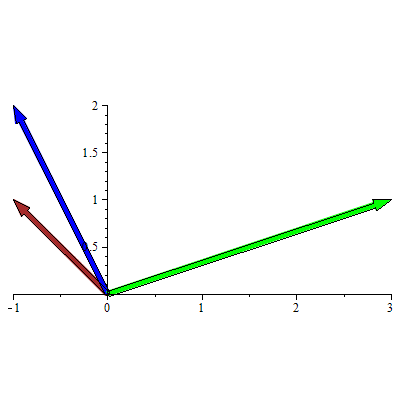
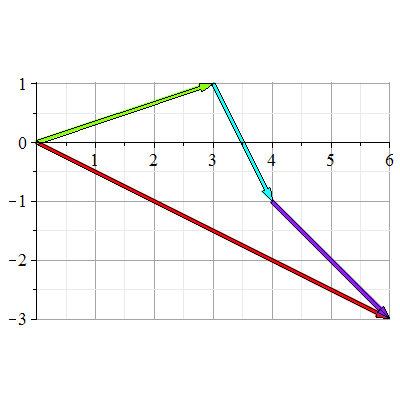
Eksempel 12
Plott vektoren 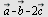 og og 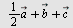 når når 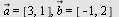 og og 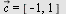
Løsning
|
| > |
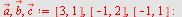 |
|
| > |
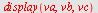 |
|
Her plottes 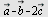
| > |
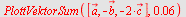 |
|
Så plotter vi 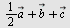 . .
| > |
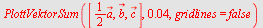 |
|
Avstand mellom punkt og linje og mellom to linjer
-
VinkelLinjeLinje
beregner vinkelen mellom to linjer
-
VinkelLinjePlan
beregner vinkelen mellom en linje og et plan
-
VinkelPlanPlan
beregner vinkelen mellom to plan
-
AvstandPunktLinje
finner avstanden fra et punkt til en linje
-
AvstandLinjeLinje
finner avstanden mellom to linjer
Eksempel 13
En linje er gitt ved parameterframstillingen 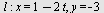 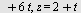
a) Finn et punkt 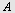 på linjen og en retningsvektor på linjen og en retningsvektor 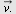
b) Finn avstanden 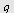 fra punktet fra punktet 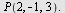
Løsning
| > |
![`assign`(l, P, [`+`(1, `-`(`*`(2, `*`(t)))), `+`(`-`(3), `*`(6, `*`(t))), `+`(2, t)], [2, -1, 3]); -1](images/utvalg_311.gif) |
|
a) Vi setter 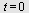 inn i inn i 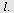
| > |
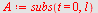 |
Retningsvektoren blir
| > |
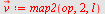 |
b)
| > |
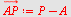 |
| > |
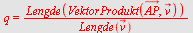 |
| > |
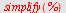 |
| > |
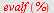 |
|
Kontroll
Med
AvstandPunktLinje
får vi
| > |
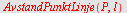 |
|
Grenseverdier
-
Grenseverdi
beregner grenseverdien av et uttrykk
Eksempel 14
Finn grenseverdien dersom den eksisterer.
a) 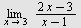  b) b) 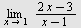
Løsning
| > |
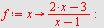 |
|
a)
| > |
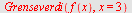 |
|
b)
| > |
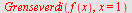 |
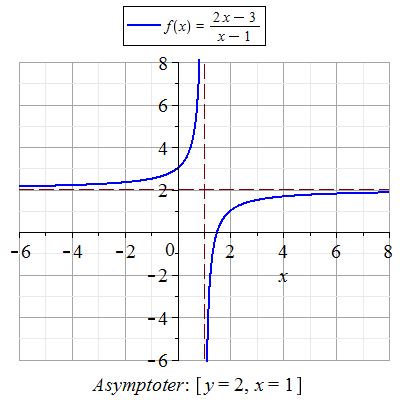
Vi benytter
Asymptote
funksjonen for å plotte grafen. Asymptoter behandles i kap. 7.
|
Vi beregner de ensidige grenseverdier.
| > |
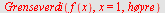 |
| > |
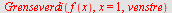 |
Se figuren til høyre.
|
| > |
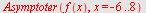 |
|
Definisjon av den deriverte
Definisjon av den deriverte
Den deriverte av 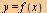 er gitt ved er gitt ved
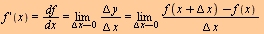
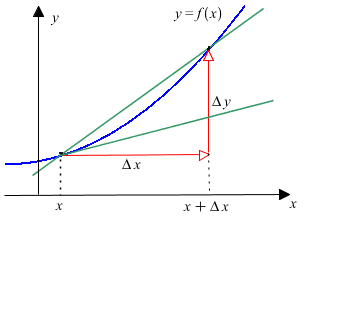
|
|
-
diff
eller
Derivere
finner den deriverte til
et uttrykk
-
Derivasjon
animerer grafene til en funksjon og dens deriverte
-
D(f)(a) eller
f'(a) finner den deriverte av
f i punktet a
-
Stigning
animerer sekanten gjennom punktene P og Q inntil sekanten faller sammen med tangenten til
f(x) i punktet P
Eksempel 15
Finn 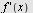 når når 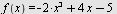
.
Hvor raskt vokser 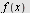 når når 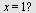
Løsning
|
| > |
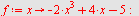 |
| > |
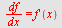 |
|
| > |
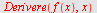 |
| > |
![(`/`(`*`(df), `*`(dx)))[x = 1] = (D(f))(1)](images/utvalg_379.gif) |
|
Vi regner ut 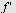 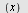 ved hjelp av definisjonen. ved hjelp av definisjonen.
|
|
| > |
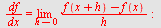 |
|
| > |
 |
|
Sammensatte funksjoner og kjerneregelen
| > |
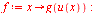 |
Kjerneregelen ligger innbakt i Maples derivasjonskommando.
|
| > |
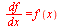 |
Her er 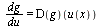
|
Eksempel 16
Regn ut 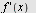 når når
a) 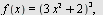 b) b) 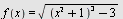 , c) , c) 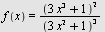
d) 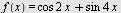 , e) , e) 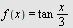 , f) , f) 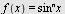
Løsning
|
a)
| > |
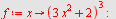 |
|
| > |
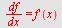 |
|
b)
| > |
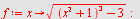 |
| > |
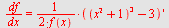 |
|
| > |
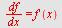 |
| > |
 |
|
c)
| > |
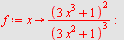 |
|
| > |
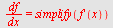 |
|
d)
| > |
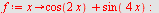 |
|
| > |
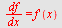 |
|
e)
| > |
 |
|
| > |
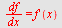 |
|
f)
| > |
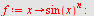 |
|
| > |
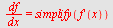 |
|
Funksjonsdrøfting
-
Funksjonsdrøfting
plotter grafen til f
, fargelegger områder med ulik krumning for f og beregner nullpunkter, kritiske punkter (ekstremalverdier), vendepunkter og randpunkter.
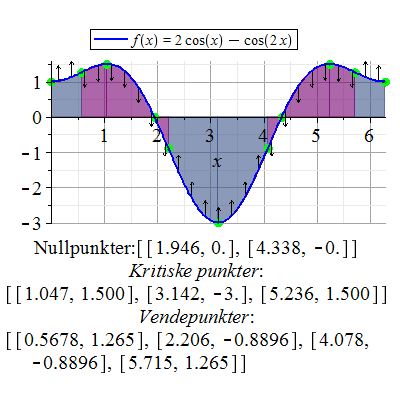
Eksempel 17
Drøft funksjonen 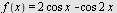 , , 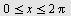
Løsning
|
a)
| > |
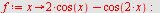 |
| > |
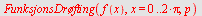 |
|
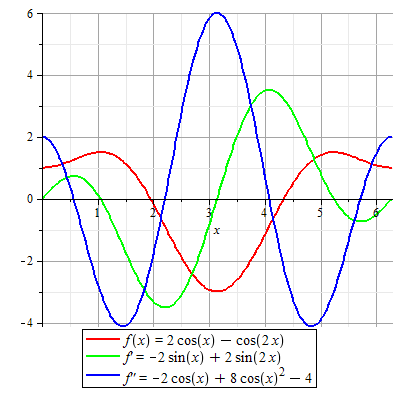
| > |
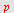 |
Her ser vi at 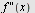 har ulik fortegn på hver side av et vendepunkt. Vi tar en test på hver side av har ulik fortegn på hver side av et vendepunkt. Vi tar en test på hver side av 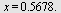
| > |
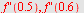 |
|
Regresjon
Begrepet regresjon eller regresjonsanalyse betegner en metode for kurvetilpasning av innsamlede data. Den desidert mest utbredte modellen er den såkalte lineære regresjonsmodellen gitt ved den rette linjen 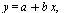 som er best mulig tilpasset observasjoner/data. Prinsippet for å finne konstantene
som er best mulig tilpasset observasjoner/data. Prinsippet for å finne konstantene 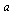 og
og 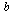 baserer seg på minste kvadraters metode. Det betyr at summen av kvadratene av vertikal avstand fra observasjonspunktene til den rette linjen skal være minst mulig.
baserer seg på minste kvadraters metode. Det betyr at summen av kvadratene av vertikal avstand fra observasjonspunktene til den rette linjen skal være minst mulig.
-
Regresjon
utfører kurvetilpasning ved minste kvadraters metode. Metodene er lineær tilpasning, eksponentiell tilpasning, potens tilpasning, polynom tilpasning, sinus tilpasning, cosinus tilpasning og fritt valgt modell tilpasning.
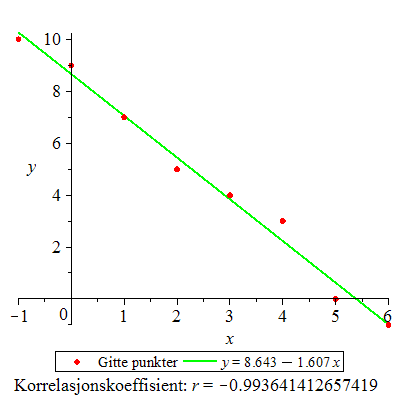
Eksempel 18
Finn minste kvadraters linje for datapunktene
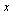
|
-1
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
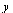
|
10
|
9
|
7
|
5
|
4
|
3
|
0
|
-1
|
Løsning
|
| > |
![`assign`(X, Y, [-1, 0, 1, 2, 3, 4, 5, 6], [10, 9, 7, 5, 4, 3, 0, -1]); -1](images/utvalg_450.gif)
![`assign`(X, Y, [-1, 0, 1, 2, 3, 4, 5, 6], [10, 9, 7, 5, 4, 3, 0, -1]); -1](images/utvalg_451.gif) |
|
| > |
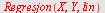 |
|
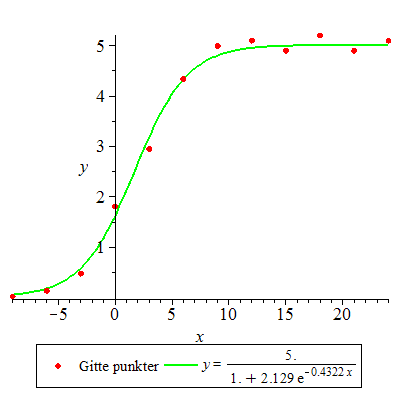
Eksempel 19
Finn en logistisk tilpasning av typen 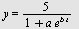 for datapunktene gitt ved for datapunktene gitt ved ![P = [[-9, 0.25e-1], [-6, .14], [-3, .48], [0, 1.81], [3, 2.95], [6, 4.34], [9, 4.99], [12, 5.1], [15, 4.9], [18, 5.2], [21, 4.9], [24, 5.1]]](images/utvalg_455.gif)
![P = [[-9, 0.25e-1], [-6, .14], [-3, .48], [0, 1.81], [3, 2.95], [6, 4.34], [9, 4.99], [12, 5.1], [15, 4.9], [18, 5.2], [21, 4.9], [24, 5.1]]](images/utvalg_456.gif)
![P = [[-9, 0.25e-1], [-6, .14], [-3, .48], [0, 1.81], [3, 2.95], [6, 4.34], [9, 4.99], [12, 5.1], [15, 4.9], [18, 5.2], [21, 4.9], [24, 5.1]]](images/utvalg_457.gif)
Løsning
|
| > |
 |
| > |
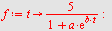 |
|
| > |
 |
|
Integrasjon
-
Integral
beregner både ubestemt og bestemt integral
-
int
beregner et ubestemt integral, men tar ikke med den vilkårlige konstanten
-
Substitusjon
utfører integrasjon ved substitusjon
-
DelvisIntegrasjon
utfører delvis integrasjon
-
DelbrøkOppspalting
utfører delbrøkoppspalting
Eksempel 20
Beregn
a) 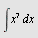 , b) , b) 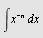 , c) , c) 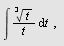 d) d) 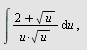 e) e) 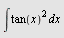
Løsning
|
a)
| > |
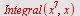 |
|
b)
| > |
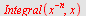 |
|
c)
| > |
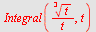 |
|
d)
| > |
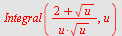 |
|
e)
| > |
 |
|
Kontroll
| > |
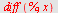 |
|
Eksempel 21
Beregn
a) 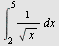 , b) , b) 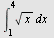 , c) , c) 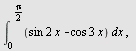 d) d) 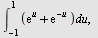
e) 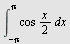
Løsning
|
a)
| > |
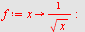 |
| > |
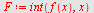 |
| > |
 |
|
| > |
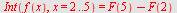 |
Direkte integrasjon
| > |
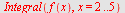 |
|
b)
| > |
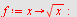 |
| > |
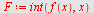 |
| > |
 |
|
| > |
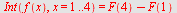 |
| > |
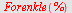 |
Direkte integrasjon
| > |
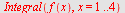 |
|
c)
| > |
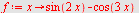 |
| > |
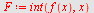 |
| > |
 |
|
| > |
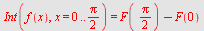 |
Direkte integrasjon
| > |
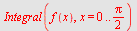 |
|
d)
| > |
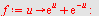 |
| > |
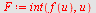 |
| > |
 |
|
| > |
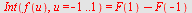 |
Direkte integrasjon
| > |
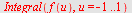 |
|
e)
| > |
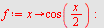 |
| > |
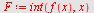 |
| > |
 |
|
| > |
 |
Direkte integrasjon
| > |
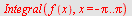 |
|
Eksempel 22
Regn ut
a) 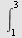 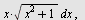 b) b) 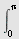 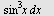
Løsning
|
a)
| > |
 |
| > |
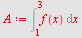 |
| > |
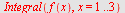 |
|
| > |
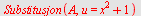 |
|
b)
| > |
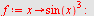 |
| > |
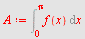 |
| > |
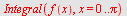 |
|
| > |
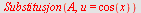 |
|
Eksempel 23
Regn ut
a) 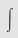 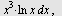 b) b) 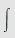 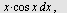 c) c) 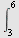 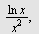 d) d)  
Løsning
a)
|
| > |
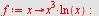 |
| > |
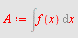 |
| > |
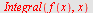 |
b)
|
Her velger vi 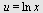
| > |
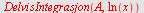 |
|
| > |
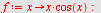 |
| > |
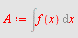 |
| > |
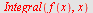 |
c)
|
Her er 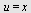
| > |
 |
|
| > |
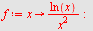 |
| > |
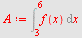 |
| > |
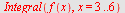 |
|
Velger 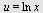
| > |
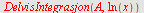 |
|
d)
| > |
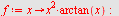 |
| > |
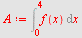 |
| > |
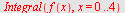 |
|
Her velger vi 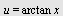
| > |
 |
|
| > |
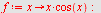 |
| > |
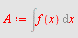 |
| > |
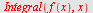 |
|
Her er 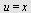
| > |
 |
|
Eksempel 24
Regn ut
a) 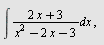 b) b) 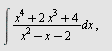 c) c) 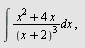
Løsning
|
a)
| > |
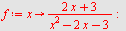 |
| > |
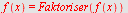 |
|
Da er
| > |
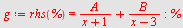 |
|
| > |
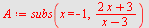 |
| > |
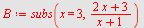 |
|
| > |
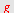 |
Med
DelbrøkOppspalting
får vi resultatet direkte
| > |
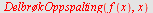 |
|
| > |
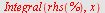 |
|
Direkte integrasjon
| > |
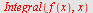 |
|
b)
| > |
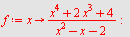 |
| > |
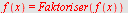 |
| > |
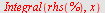 |
|
| > |
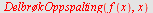 |
| > |
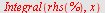 |
|
c)
| > |
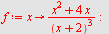 |
| > |
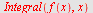 |
|
| > |
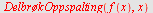 |
| > |
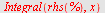 |
|
Volum av omdreiningslegemer
-
RotasjonsVolum
plotter og beregner volumet av et omdreiningslegeme
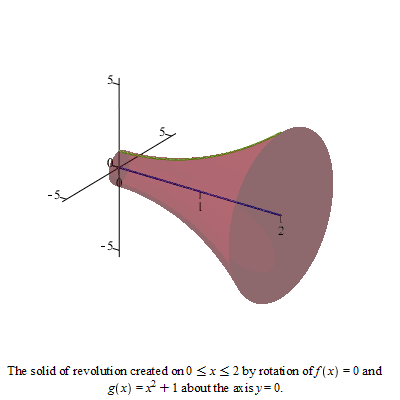
Eksempel 25
Beregen volumet av det legemet som framkommer ved at flatestykket mellom 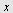 -aksen og kurven roterer om -aksen og kurven roterer om 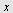 -aksen når -aksen når
a) 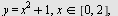 b) b) 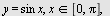 c) c) ![y = `*`(ln, `*`(x)), `in`(x, [0, e])](images/utvalg_658.gif)
Løsning
a)
|
| > |
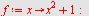 |
Volumet er da gitt ved
| > |
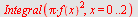 |
Eller ved
| > |
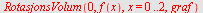 |
|
| > |
 |
Klikk på figuren og drei på den.
|
b)
| > |
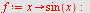 |
Volumet er da gitt ved
| > |
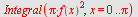 |
Eller ved
| > |
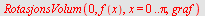 |
|
| > |
 |
Klikk på figuren og drei på den.
|
c)
| > |
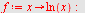 |
Volumet er da gitt ved
| > |
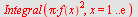 |
Eller ved
| > |
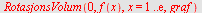 |
|
| > |
 |
Klikk på figuren og drei på den.
|
Differensialligninger og løsningskurver
-
LøsDiffLigning
eller
dsolve
løser differensialligninger
Eksempel 26
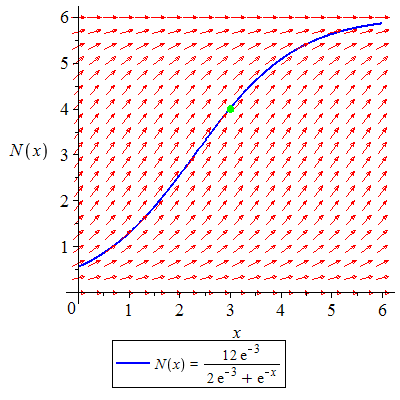
a) Løs differensialligningen 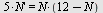
b) Løs differensialligningen 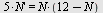 , , 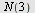 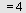
Plott retningsdiagrammet og grafen til 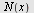 for for ![`in`(x, [0, 6])](images/utvalg_688.gif)
c) Beregn grenseverdien for 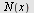 når når 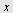 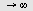
d) Finn vekstfarten når 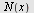 = 4 = 4
Løsning
|
a)
| > |
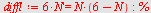 |
Den generelle løsningen er
| > |
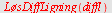 |
Retningsdiagrammet blir
| > |
 |
|
b)
| > |
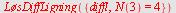 |
| > |
![LøsDiffLigning([diffl, N(3) = 4], x = 0 .. 6, N = 0 .. 6)](images/utvalg_701.gif) |
|
c)
| > |
![`assign`(N, proc (x) options operator, arrow; `+`(`/`(`*`(6), `*`(`+`(`*`(6, `*`(c[1], `*`(exp(`+`(`-`(x)))))), 1)))) end proc); -1](images/utvalg_704.gif) |
| > |
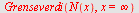 |
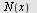 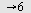 når når 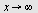
| > |
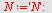 |
|
d)
| > |
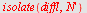 |
Vi setter inn 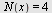 på høyre side og får vekstfarten på høyre side og får vekstfarten
| > |
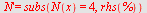 |
|
Eulers metode
-
EulersMetode
viser den numeriske løsningen med Eulers metode ved animasjon
-
LøsDiffLigning
løser en differensialligning både eksakt og numerisk og plotter retningsdiagrammet til en første ordens differensialligning når intervallene for
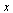 og
og 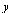 er gitt
er gitt
| > |
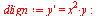 |
| > |
 |
Vi får retningsdiagrammet med
| > |
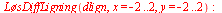 |
|
| > |
 |
|
| > |
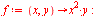 |
| > |
 |
Klikk på figuren og start animasjonen.
|
| > |
![feil[1 .. 10]](images/utvalg_738.gif) |
|
Eksempel 27
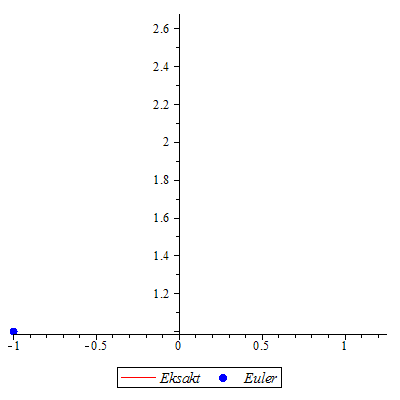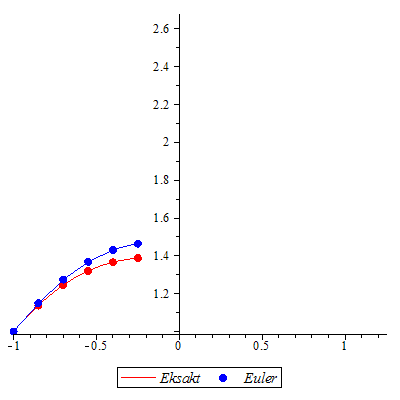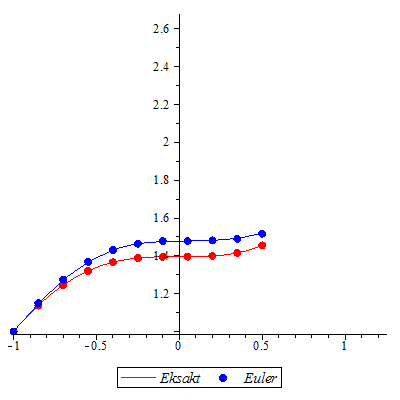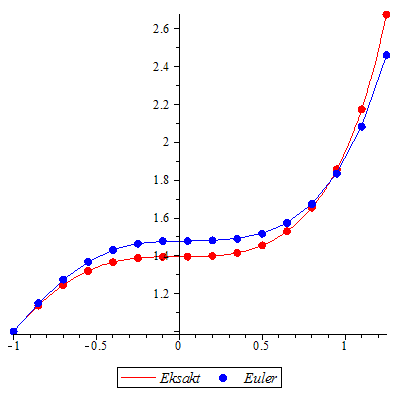
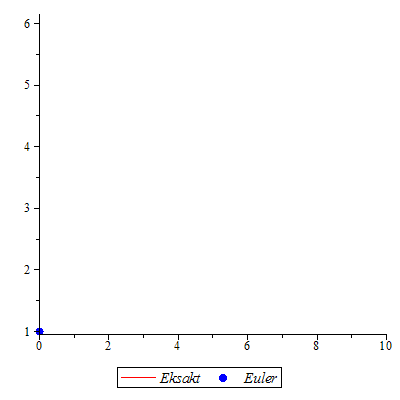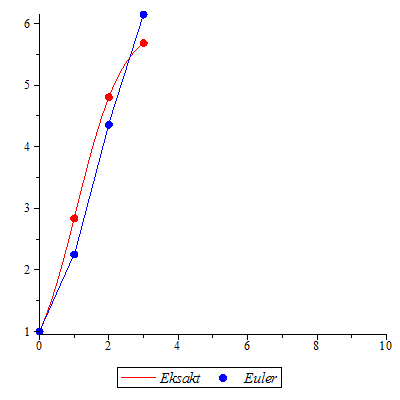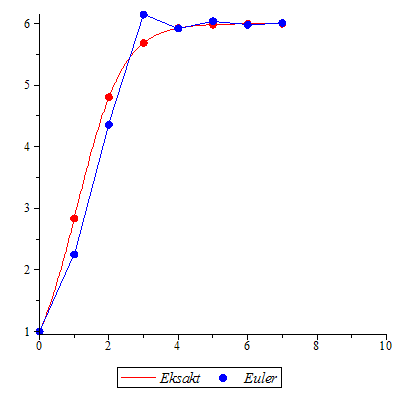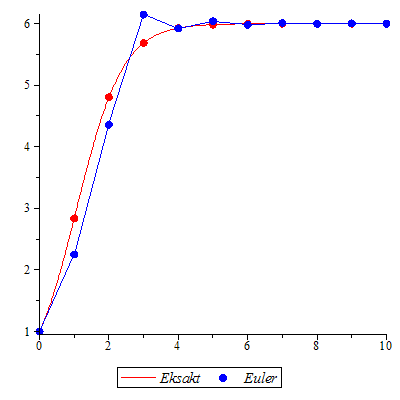
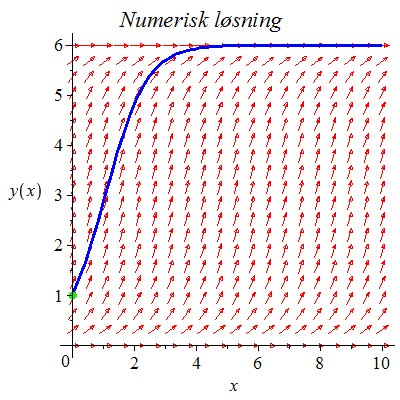
Løs differensialligningen ved Eulers metode.
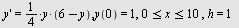 og ved "eksakt" numerisk metod og ved "eksakt" numerisk metod
|
Løsning
| > |
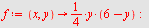 |
| > |
 |
Klikk på figuren og start animasjonen.
|
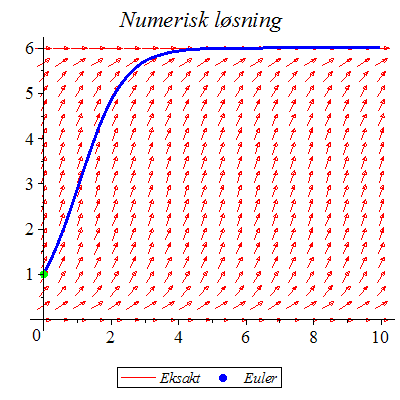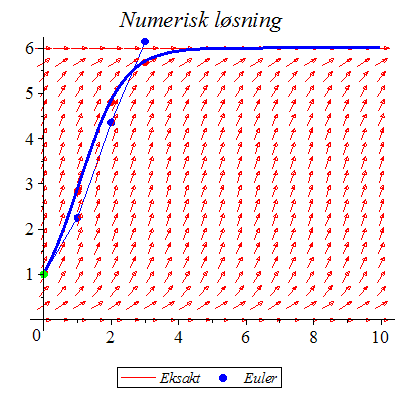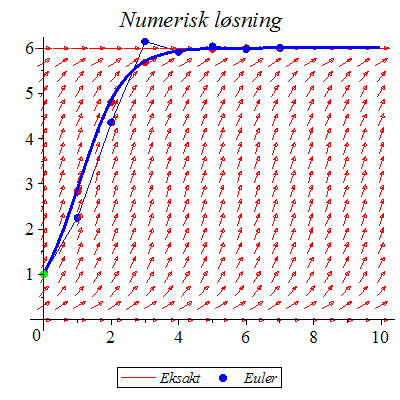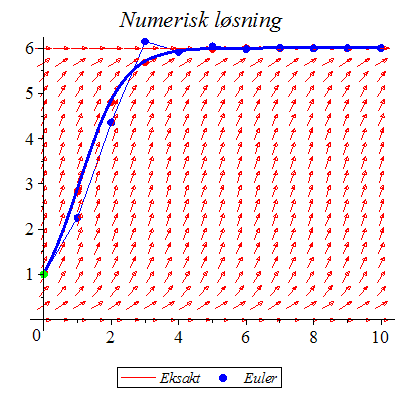
"Eksakt" numerisk metode
| > |
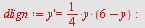 |
| > |
![`assign`(p2, LøsDiffLigning([dlign, y(0) = 1], x = 0 .. 10, y = 0 .. 6, numerisk)); -1; %](images/utvalg_745.gif)
![`assign`(p2, LøsDiffLigning([dlign, y(0) = 1], x = 0 .. 10, y = 0 .. 6, numerisk)); -1; %](images/utvalg_746.gif) |
|
| > |
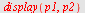 |
Den eksakte løsningen faller sammen med den "eksakte" numeriske løsningen.
Klikk på figuren og start animasjonen.
|
|
|
Aritmetiske og geometriske rekker
-
AritmetiskRekke
beregner det nte leddet
![a[n]](images/utvalg_750.gif) og summen
og summen ![s[n]](images/utvalg_751.gif)
-
GeometriskRekke
beregner det nte leddet
![a[n]](images/utvalg_752.gif) og summen
og summen ![s[n]](images/utvalg_753.gif)
Eksempel 28
I en aritmetisk rekke er første ledd 4 og differansen er 2.
a) Finn ledd nr 200.
b) Finn en formel for ledd nr n, ![a[n]](images/utvalg_754.gif) . .
c) Finn en formel for summen av de 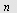 første leddene, første leddene, ![s[n]](images/utvalg_756.gif) . .
Finn 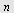 når når ![s[n] = 18904](images/utvalg_758.gif)
Løsning
|
a)
| > |
![`assign`(a[1], d, 4, 2); -1](images/utvalg_759.gif) |
| > |
![a[200] = `+`(a[1], `*`(`+`(200, -1), `*`(d)))](images/utvalg_760.gif) |
eller
| > |
 |
|
b)
| > |
![a[n] = `+`(a[1], `*`(`+`(n, `-`(1)), `*`(d)))](images/utvalg_765.gif) |
eller med
| > |
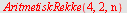 |
|
c)
| > |
![s[n] = `+`(`*`(`/`(1, 2), `*`(`+`(a[1], 2, `*`(2, `*`(n))), `*`(n))))](images/utvalg_770.gif) |
|
| > |
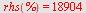 |
| > |
 |
Antall ledd er 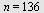
|
Eksempel 29
I en geometrisk tallfølge er ![a[1] = 5](images/utvalg_777.gif) og og 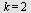 . .
a) Finn ledd nr 8.
b) Hvilket nummer i følgen har leddet 327680?
Løsning
|
a)
| > |
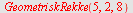 |
|
b)
| > |
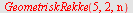 |
|
| > |
![a[n] = `+`(`*`(5, `*`(`^`(2, `+`(n, `-`(1)))))); -1](images/utvalg_785.gif) |
| > |
![subs(a[n] = 327680, %)](images/utvalg_786.gif) |
|
| > |
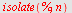 |
|
Konvergens og uendelige rekker
Eksempel 30
Finn konvergensområdet og regn ut summen av rekken
a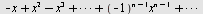
b) 1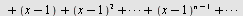
Løsning
|
a)
| > |
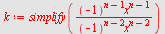 |
| > |
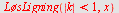 |
Konvergensområdet er for 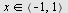
|
| > |
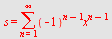 |
eller ved formelen
| > |
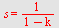 |
|
b)
| > |
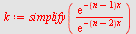 |
| > |
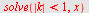 |
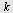 er alltid positiv. er alltid positiv.
| > |
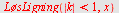 |
Konvergensområdet er for 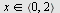
|
| > |
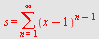 |
eller ved formelen
| > |
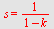 |
|
Binomialkoeffisienter
Eksempel 31
a) Beregn Beregn 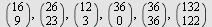
b) Skriv opp de første 9 og 11 rekker i Pascals trekant
c) 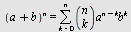 for for 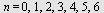
Løsning
a)
| > |
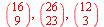 |
|
| > |
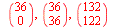 |
|
b)
| > |
 |
|
| > |
 |
|
c)
| > |
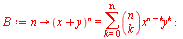 |
| > |
 |
| > |
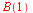 |
| > |
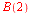 |
| > |
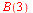 |
|
| > |
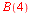 |
| > |
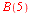 |
| > |
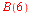 |
| > |
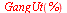 |
|
|
Simulering
Simulering av kast med en terning kan gjøres i Maple med kommandoen
rand
.
-
rand
( ) gir et tilfeldig tall med 12 siffer
rand(a,b)()
gir et tilfeldig tall mellom a og b
eller med tilsvarende kommandoer i pakken
vgs
,
-
TilfeldigTall
gir et tilfeldig tall
-
Histogram
plotter et histogram
-
StolpeDiagram
plotter et histogram med enten absolutte eller relative frekvenser
-
FrekvensTabell
skriver ut en frekvenstabell
Normalfordeling
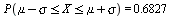
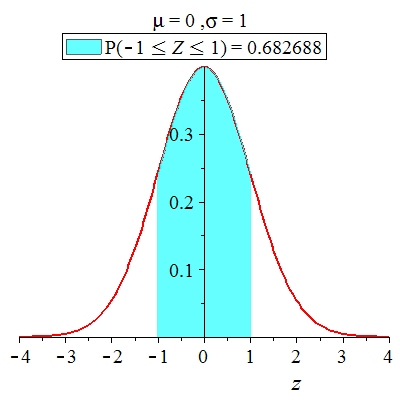
| > |
 |
ca 68.27% av observasjonene ligger mindre enn ett standardavvik fra middelverdien 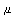
|
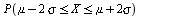

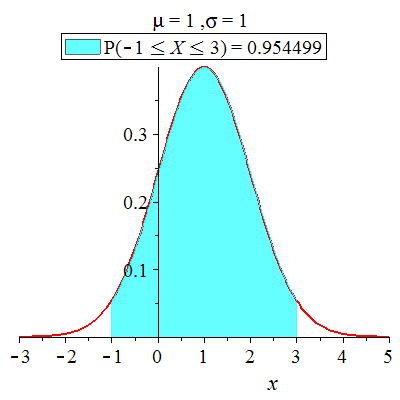
| > |
 |
ca 95.45% av observasjonene ligger mindre enn to standardavvik fra middelverdien 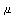
|
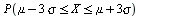

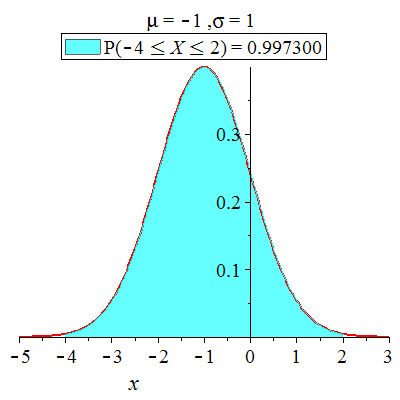
| > |
 |
ca 99.73 % av observasjonene ligger mindre enn tre standardavvik fra middelverdien 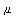
|
Statistikk
Noen kommandoer i
vgs
-pakken er:
-
Middelverdi
,
Standardavvik
,
Varians
,
Typetall
,
Prosentil
,
Desil
,
Kvartil
,
Medianen
,
MidlereAvvik
,
StolpeDiagram
,
KumulativeFrekvenser
,
FrekvensTabell
,
KlasseInndeling
,
SumfordelingsDiagram
Eksempel 34
Gitt ![[6, 3, 6, 6, 2, 5, 3, 5, 6, 6, 10, 4, 7, 4, 2, 3, 1, 12, 7, 2, 3, 3, 4, 10, 8, 2]](images/utvalg_890.gif)
a) Lag en frekvenstabell.
b) Finn variasjonsbredden.
c) Finn hyppigste verdi og regn ut gjennomsnittet.
d) Tegn et stolpediagram.
Løsning
| > |
![`assign`(L, [6, 3, 6, 6, 2, 5, 3, 5, 6, 6, 10, 4, 7, 4, 2, 3, 1, 12, 7, 2, 3, 3, 4, 10, 8, 2]); -1; %](images/utvalg_891.gif) |
| > |
 |
a)
| > |
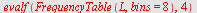 |
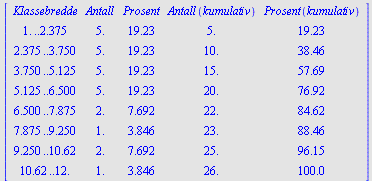
Vi får samme verdier med
FrekvensTabell
, men vi får også informasjon om hva kolonnene står for.
| > |
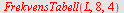 |
b) Variasjonsbredden er
| > |
 |
|
| > |
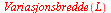 |
|
c) Med
Mode
får vi bare det ene typetallet.
| > |
 |
|
| > |
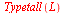 |
gir begge typetallene og også hyppigheten eller frekvensen.
| > |
 |
|
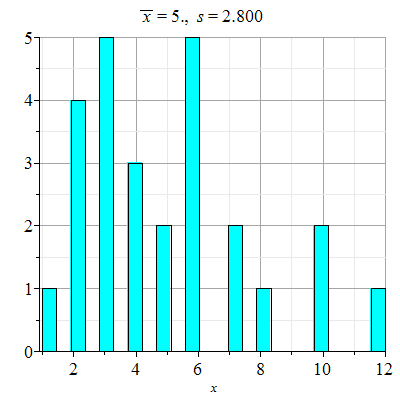
d)
| > |
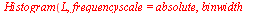
 |
Høyden på hver av søylene angir tallets hyppighet. Bredden på søylene angis med binwidth.
|
| > |
 |
|
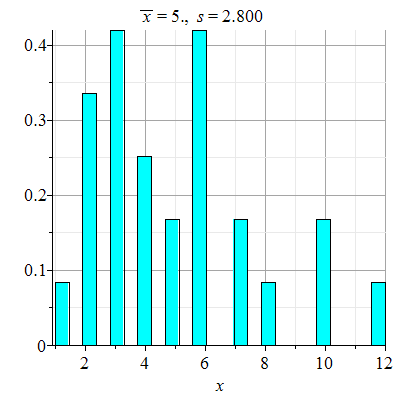
| > |
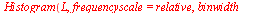
 |
Med angivelsen relative er summen av søylenes areal lik 1
|
| > |
 |
|
|
Logikk
Maple har følgende
logiske operatorer
:
- not er kommandoen for negasjon
- or er kommandoen for disjunksjon
- and er kommandoen for konjunksjon
-
SannhetsTabell
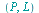 setter opp en sannhetsverditabell for utsagnet P og en liste L med utsagnsvariable. I tabellen står S for sant og U for usant.
setter opp en sannhetsverditabell for utsagnet P og en liste L med utsagnsvariable. I tabellen står S for sant og U for usant.
 gjør nevneren i en brøk rasjonal
gjør nevneren i en brøk rasjonal
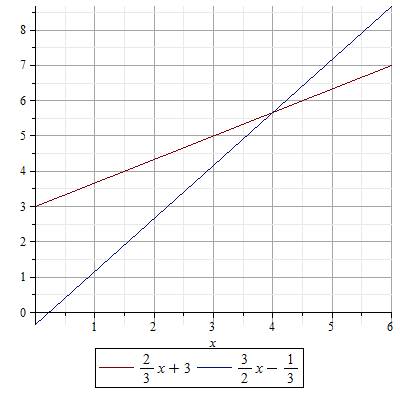



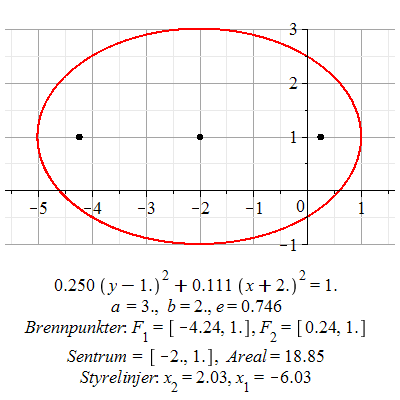
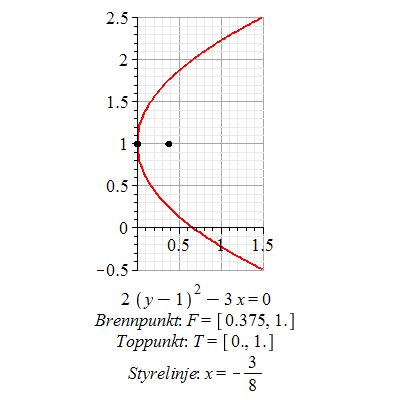
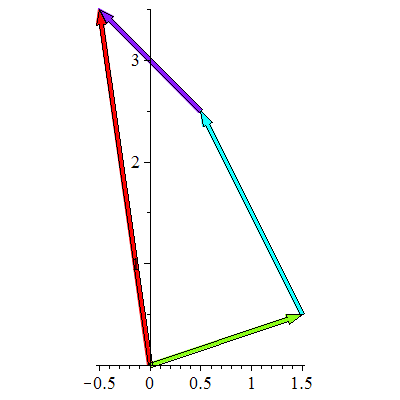

 e)
e)  d)
d) 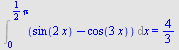
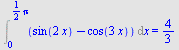
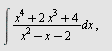 c)
c)