Multiple Integration
The regions shown in the figure below are called region of type I and region of type II.
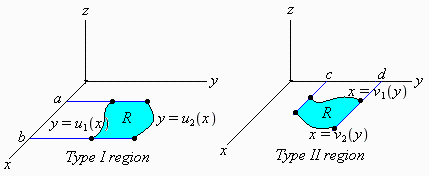
Type I region
|
Type II region
|
If ![]() is continuous on a region of Type I (vertically simple), we define an iterated integral of
is continuous on a region of Type I (vertically simple), we define an iterated integral of ![]() over the region by
over the region by
![]()
![]()
![]()
![]()
![]() dx
dx
We first integrate ![]() treating
treating ![]() in the integrand as a constant. The result of this integration is a function of
in the integrand as a constant. The result of this integration is a function of ![]() say
say ![]() Next, integrate
Next, integrate ![]()
![]() . This final result is the value of the iterated integral. The basic idea is to carry out successive integrations.
. This final result is the value of the iterated integral. The basic idea is to carry out successive integrations.
In a similar manner, we define an iterated integral of a continuous function ![]() over a region of Type II (horizontally simple) by
over a region of Type II (horizontally simple) by
![]()
![]() dy =
dy =![]()
![]()
![]()
![]()
![]() dy
dy
Iterated integrals provide the means for evaluating a double integral ![]()
![]() over a region of Type I or Type II or a region that can be expressed as a union of a finite number of these regions.
over a region of Type I or Type II or a region that can be expressed as a union of a finite number of these regions.
Evaluation of Double Integrals
Let ![]() be continuous on a region
be continuous on a region ![]()
- If
 is of Type I, then
is of Type I, then
![]()
![]()
![]()
- If
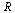 is of Type II, then
is of Type II, then
![]()
![]()
![]()
![]() dy
dy
Evaluation of Double Integrals
-
Doubleint
(
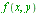 ,
,![x = x[1]](images/Some Pages_689.gif) ..
..![x[2]](images/Some Pages_690.gif) ,
, ![y = y[1]](images/Some Pages_691.gif) ..
..![y[2]](images/Some Pages_692.gif) ) is an inert form of double integration. Use
value
(Doubleint(...) to force Doubleint to evaluate like
int
.
) is an inert form of double integration. Use
value
(Doubleint(...) to force Doubleint to evaluate like
int
.
We can also calculate the iterated integral using
-
int
(
int
(
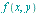 ,
, ![x = x[1]](images/Some Pages_694.gif) ..
..![x[2]](images/Some Pages_695.gif) ),
), ![y = y[1]](images/Some Pages_696.gif) ..
..![y[2]](images/Some Pages_697.gif) )
)
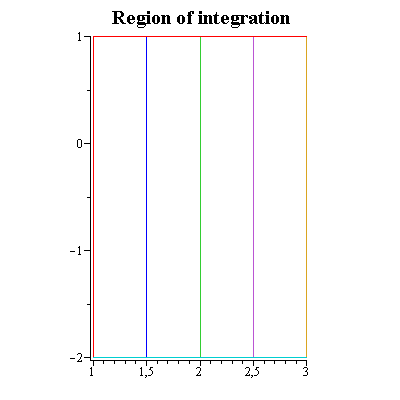
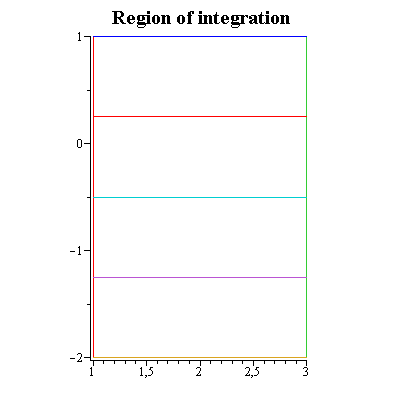
As an aid in reducing a double integral to an iterated integral with correct limits of integration, it is useful to visualize the double summation process pictorially. This can be indicated by vertical lines in region of Types I and horizontally lines in region of Types II.
In the package calcplot , you will find commands for plotting such 2D regions described in Cartesian coordinates.
-
dxdyplot
(
 .. x[2](y), y = c .. d](images/Some Pages_698.gif) ) plots the region in the plane with the given arguments as boundary curves
) plots the region in the plane with the given arguments as boundary curves
-
dydxplot
(
 .. y[2](x), x = a .. b](images/Some Pages_699.gif) ) plots the region in the plane with the given arguments as boundary curves
) plots the region in the plane with the given arguments as boundary curves
Example 1
Compute the iterated integrals
![]() ,
, ![]()
Solution
a)
Region of integration
The line segments that pass through the interior of the region illustrate elements of integration.
|
Now we evaluate the integral by reversing the order of integration.
We calculate the integral by first integrating from
|