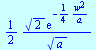Fourier Transforms
The ability to analyze various types of waveforms is an important engineering skill. Both the Laplace transform and the Fourier transform are important integral transforms in engineering.
Fourier transform is used extensively in communications engineering and signal processing.
The Fourier transform can be obtained from the complex Fourier integral representation in the foregoing section. The complex Fourier integral
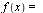
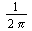
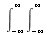
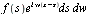
can be rewritten as an iterated integral
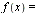
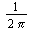
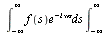
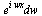
The variable 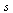 is a dummy variable and will be replaced by
is a dummy variable and will be replaced by 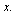 Thus we have a pair of integrals called a Fourier transform pair.
Thus we have a pair of integrals called a Fourier transform pair.
Fourier Transform Pair
- The Fourier transform of
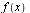 is denoted
is denoted 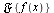 or
or 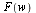 and defined by
and defined by
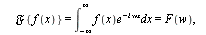
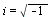
- The inverse Fourier transform of
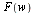 is denoted
is denoted 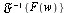
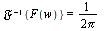
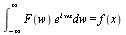
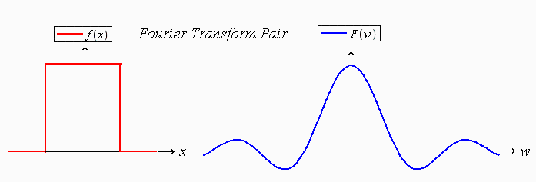
Fourier Transform Pair
Note: The scaling factor 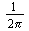 in the second integral is fairly standard (also used by Maple). But some authors in math textbooks write the factor
in the second integral is fairly standard (also used by Maple). But some authors in math textbooks write the factor 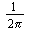 in the first integral while others place a factor
in the first integral while others place a factor 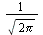 in both giving some symmetry to the equations. In all cases the pair combine to give the the complex Fourier integral.
in both giving some symmetry to the equations. In all cases the pair combine to give the the complex Fourier integral.
The Fourier sine and cosine integral pairs can also be interpreted as pairs of mutually inverse transforms. For reasons of symmetry, this is usually done by splitting the numerical factor  in
in 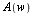 and
and 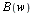 into two equal factors and assigning one factor to each integral in the pair.
into two equal factors and assigning one factor to each integral in the pair.
Fourier Cosine and Sine Transform Pairs
- The Fourier cosine transform of
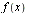 is denoted
is denoted ![`*`(`𝔉`[c], `*`({f(x)}))](images/Some Pages_371.gif) or
or ](images/Some Pages_372.gif) and defined by
and defined by
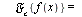
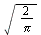
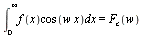
- The inverse Fourier cosine transform of
](images/Some Pages_376.gif) is denoted
is denoted }), `*`(`𝔉`[c]))](images/Some Pages_377.gif)
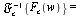
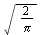
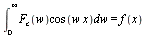
- The Fourier sine transform of
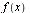 is denoted
is denoted ![`*`(`𝔉`[s], `*`({f(x)}))](images/Some Pages_382.gif) or
or ](images/Some Pages_383.gif) and defined by
and defined by
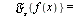
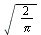
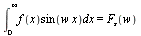
- The inverse Fourier sine transform of
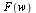 is denoted
is denoted ![`/`(`*`({F(w)}), `*`(`𝔉`[s]))](images/Some Pages_388.gif)
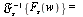
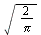
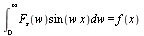
Fourier Cosine and Sine Transform Pairs
-
fourier
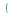
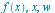
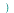 applies the Fourier transform to
applies the Fourier transform to 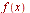 with respect to
with respect to 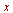
-
invfourier
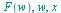
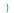 applies the inverse Fourier transform to
applies the inverse Fourier transform to 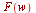 with respect to
with respect to 
-
fouriercos
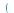
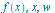
 applies the Fourier cosine transform to
applies the Fourier cosine transform to 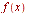 with respect to
with respect to 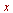
-
fouriercos
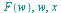
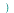 applies the inverse Fourier cosine transform to
applies the inverse Fourier cosine transform to 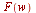 with respect to
with respect to 
-
fouriersin
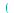
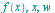
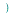 applies the Fourier cosine transform to
applies the Fourier cosine transform to 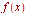 with respect to
with respect to 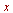
-
fouriersin
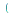
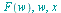
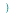 applies the inverse Fourier cosine transform to
applies the inverse Fourier cosine transform to 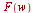 with respect to
with respect to 
Note: The
fouriercos
and
fouriersin
commands are self-inverting.
When we use Maple, the Fourier transform, the inverse Fourier transform, the Fourier cosine transform, and the Fourier sine transform operators 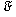 ,
,![`/`(1, `*`(`𝔉`)), `𝔉`[c]](images/Some Pages_423.gif) , and
, and 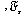 are replaced by
are replaced by 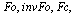 and
and 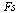 , respectively.
, respectively.
To facilitate the use of these operators, as defined below, they are included in the initialization procedure.
| > |
restart:MathMaple:-ini(): |
| > |
Fo:=f->fourier(f,x,w):
invFo:=F->invfourier(F,w,x):
alias(F(w)=Fo(f(x)),G(w)=Fo(g(x))): |
| > |
Fs:=f->fouriersin(f,x,w):
invFs:=F->fouriersin(F,w,x):
Fc:=f->fouriercos(f,x,w):
invFc:=F->fouriercos(F,w,x):
alias(F[s](w)=Fs(f(x)),F[c](w)=Fc(f(x))): |
|
|
| > |
'invFo'(F(w))=invFo(F(w)); |
|
|
|
| > |
'invFs'(F[s](w))=invFs(F[s](w)); |
|
|
|
| > |
'invFc'(F[c](w))=invFc(F[c](w)); |
|
-
convert
 converts a transform to an inert integral representation
converts a transform to an inert integral representation
Fourier transform
| > |
F(w)=convert(fourier(f(x),x,w),Int); |
|
Inverse Fourier transform
| > |
f(x)=convert(invfourier('F'(w),w,x),Int); |
|
Fourier sine transform
| > |
F[s](w)=convert(fouriersin(f(x),x,w),Int); |
|
Inverse Fourier sine transform
| > |
f(x)=convert(fouriersin('F'[s](w),w,x),Int); |
|
Fourier cosine transform
| > |
F[c](w)=convert(fouriercos(f(x),x,w),Int); |
|
Inverse Fourier cosine transform
| > |
f(x)=convert(fouriercos('F'[c](w),w,x),Int); |
|
Fourier transforms of some basic functions
|
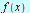
|
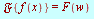
|
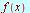
|
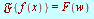
|
|
|
|
|
|
|
|
|
| > |
f:=piecewise(x>b and x<c,exp(a*x),0); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| > |
exp(I*a*x)*(H(x+b)-H(x-b)); |
|
|
|
|
Fourier cosine transforms of some basic functions
|
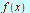
|
![`*`(`𝔉`[c], `*`({f(x)})) = F[c](w)](images/Some Pages_475.gif)
|
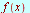
|
![`*`(`𝔉`[c], `*`({f(x)})) = F[c](w)](images/Some Pages_477.gif)
|
| > |
f:=piecewise(x>0 and x<a,1,0): |
|
|
|
|
|
|
|
| > |
assume(a>0):
exp(-a*x^2); |
|
|
|
|
|
|
|
|
|
|
|
|
Fourier sine transforms of some basic functions
|
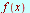
|
![`*`(`𝔉`[s], `*`({f(x)})) = F[s](w)](images/Some Pages_499.gif)
|
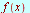
|
![`*`(`𝔉`[s], `*`({f(x)})) = F[s](w)](images/Some Pages_501.gif)
|
| > |
f:=piecewise(x>0 and x<a,1,0): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| > |
assume(a>0):
arctan(2*a/x); |
|
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() is a dummy variable and will be replaced by
is a dummy variable and will be replaced by ![]() Thus we have a pair of integrals called a Fourier transform pair.
Thus we have a pair of integrals called a Fourier transform pair. 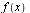 is denoted
is denoted 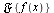 or
or 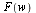 and defined by
and defined by![]()
![]()
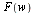 is denoted
is denoted 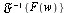
![]()
![]()

![]() in the second integral is fairly standard (also used by Maple). But some authors in math textbooks write the factor
in the second integral is fairly standard (also used by Maple). But some authors in math textbooks write the factor ![]() in the first integral while others place a factor
in the first integral while others place a factor ![]() in both giving some symmetry to the equations. In all cases the pair combine to give the the complex Fourier integral.
in both giving some symmetry to the equations. In all cases the pair combine to give the the complex Fourier integral. ![]() in
in ![]() and
and ![]() into two equal factors and assigning one factor to each integral in the pair.
into two equal factors and assigning one factor to each integral in the pair. 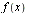 is denoted
is denoted ![`*`(`𝔉`[c], `*`({f(x)}))](images/Some Pages_371.gif) or
or ](images/Some Pages_372.gif) and defined by
and defined by![]()
![]()
![]()
](images/Some Pages_376.gif) is denoted
is denoted }), `*`(`𝔉`[c]))](images/Some Pages_377.gif)
![]()
![]()
![]()
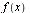 is denoted
is denoted ![`*`(`𝔉`[s], `*`({f(x)}))](images/Some Pages_382.gif) or
or ](images/Some Pages_383.gif) and defined by
and defined by![]()
![]()
![]()
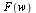 is denoted
is denoted ![`/`(`*`({F(w)}), `*`(`𝔉`[s]))](images/Some Pages_388.gif)
![]()
![]()
![]()
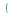
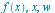
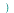 applies the Fourier transform to
applies the Fourier transform to 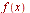 with respect to
with respect to 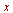
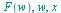
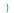 applies the inverse Fourier transform to
applies the inverse Fourier transform to 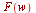 with respect to
with respect to 
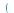
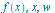
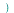 applies the Fourier cosine transform to
applies the Fourier cosine transform to 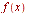 with respect to
with respect to 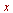
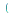
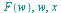
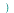 applies the inverse Fourier cosine transform to
applies the inverse Fourier cosine transform to 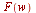 with respect to
with respect to 
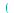
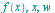
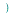 applies the Fourier cosine transform to
applies the Fourier cosine transform to 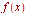 with respect to
with respect to 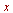
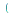
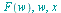
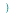 applies the inverse Fourier cosine transform to
applies the inverse Fourier cosine transform to 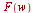 with respect to
with respect to 
![]() ,
,![]() , and
, and ![]() are replaced by
are replaced by ![]() and
and ![]() , respectively.
, respectively.  converts a transform to an inert integral representation
converts a transform to an inert integral representation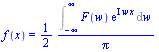
 = `/`(`*`(`^`(2, `/`(1, 2)), `*`(Int(`*`(f(x), `*`(sin(`*`(x, `*`(w))))), x = 0 .. infinity))), `*`(`^`(Pi, `/`(1, 2))))](images/Some Pages_436.gif)
, `*`(sin(`*`(x, `*`(w))))), w = 0 .. infinity))), `*`(`^`(Pi, `/`(1, 2))))](images/Some Pages_437.gif)
 = `/`(`*`(`^`(2, `/`(1, 2)), `*`(Int(`*`(f(x), `*`(cos(`*`(x, `*`(w))))), x = 0 .. infinity))), `*`(`^`(Pi, `/`(1, 2))))](images/Some Pages_438.gif)
, `*`(cos(`*`(x, `*`(w))))), w = 0 .. infinity))), `*`(`^`(Pi, `/`(1, 2))))](images/Some Pages_439.gif)