The response of a mass-spring system to an impulse function
As said above the Dirac delta function could serve as a mathematical model for an external force of large magntiude that acts for only a very short period of time..
| > |
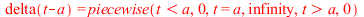 |
where
| > |
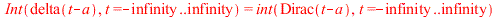 |
Obviously no real function can satisfy beeing zero except at a single point and have an integral equal to one.
In Maple 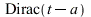 is expressed as the derivative of the Heaviside standard unit step function.
is expressed as the derivative of the Heaviside standard unit step function.
| > |
 |
| > |
 |
It is instructive to use Maple to model such an instantaneous unit impulse by starting with the function
| > |
)) = piecewise(`<`(t, a), 0, `<`(t, `+`(a, epsilon)), `/`(1, `*`(epsilon)), 0)](images/paper_151.gif) |
| > |
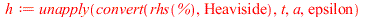 |
A plot of the rectangular pulse for 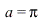 and
and 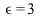 gives
gives
| > |
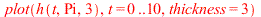 |
The area of the rectangular pulse is equal to 1.
| > |
 |
| > |
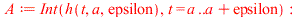 |
| > |
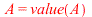 |
where 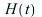 is Heavisides unit step function. We can compare the response of a damped mass-spring system to a rectangular pulse
is Heavisides unit step function. We can compare the response of a damped mass-spring system to a rectangular pulse ))](images/paper_164.gif) as
as 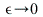 with the response of the Dirac's delta function used by Maple.
with the response of the Dirac's delta function used by Maple.
The output of the Maple code impulse_func (written above) animates the response to the rectangular pulse ))](images/paper_166.gif) by a linear second order differential equation with constant coefficients and with damping.
by a linear second order differential equation with constant coefficients and with damping.
| > |
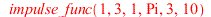 |
Animation
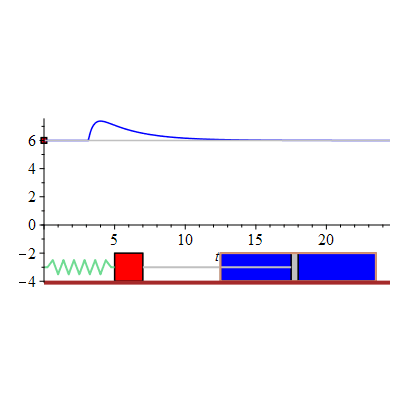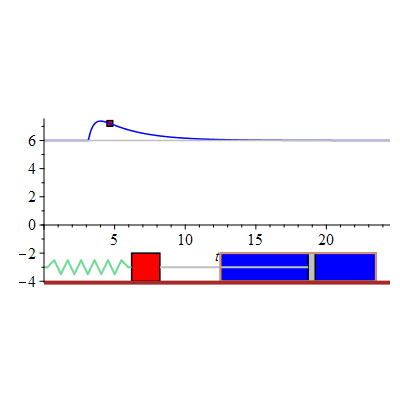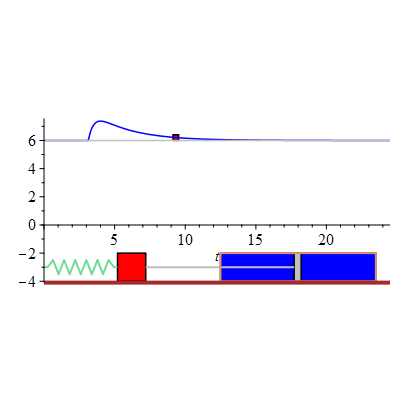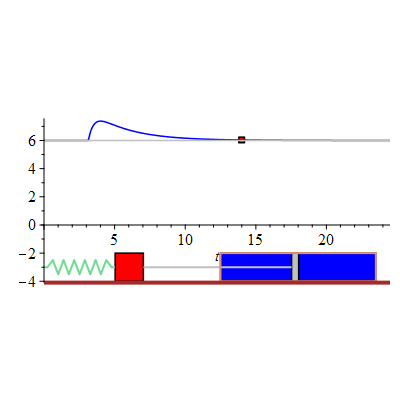
The behavior of the response to a rectangular pulse by a linear second order differential equation with damping as 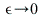 compared to the response to Dirac's delta function.
compared to the response to Dirac's delta function.
The last animated frame shows little difference between the two responses when 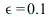
| > |
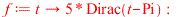 |
| > |
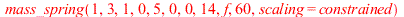 |
The figure shows an animated response of the damped mass-spring system initially at rest. At time 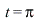 the system is suddenly given a sharp "hammerblow" modelled by
the system is suddenly given a sharp "hammerblow" modelled by 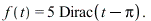
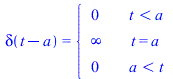
![]() is expressed as the derivative of the Heaviside standard unit step function.
is expressed as the derivative of the Heaviside standard unit step function. )) = piecewise(`<`(t, a), 0, `<`(t, `+`(a, epsilon)), `/`(1, `*`(epsilon)), 0)](images/paper_152.gif)
![]() and
and ![]() gives
gives 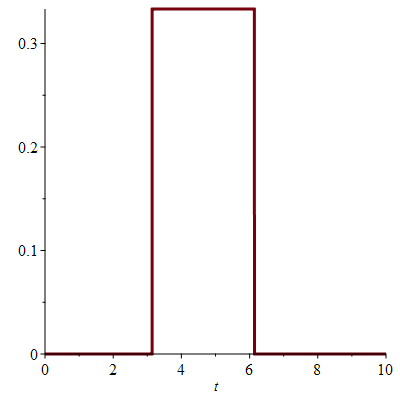
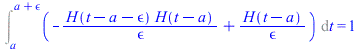
![]() is Heavisides unit step function. We can compare the response of a damped mass-spring system to a rectangular pulse
is Heavisides unit step function. We can compare the response of a damped mass-spring system to a rectangular pulse ![]() as
as ![]() with the response of the Dirac's delta function used by Maple.
with the response of the Dirac's delta function used by Maple.
![]() by a linear second order differential equation with constant coefficients and with damping.
by a linear second order differential equation with constant coefficients and with damping. 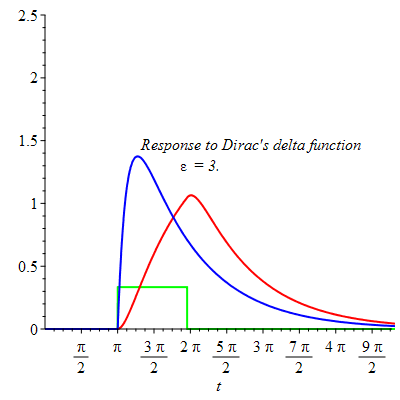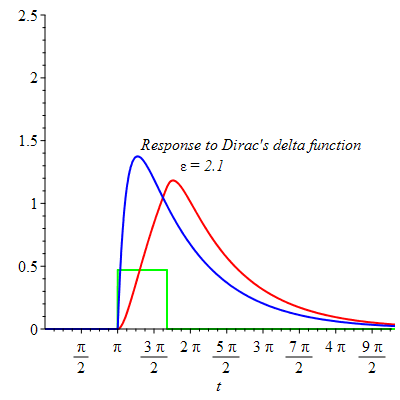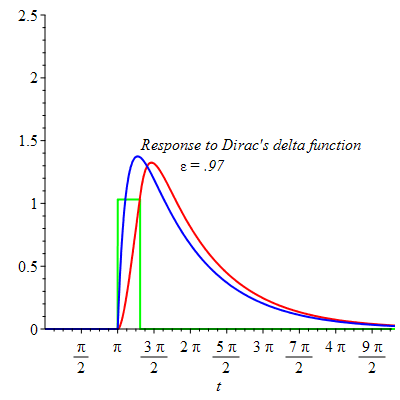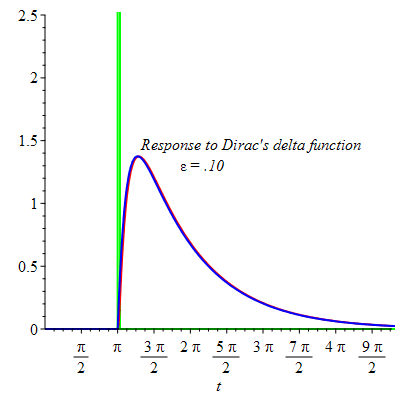
![]() compared to the response to Dirac's delta function.
compared to the response to Dirac's delta function. ![]()
![]() the system is suddenly given a sharp "hammerblow" modelled by
the system is suddenly given a sharp "hammerblow" modelled by ![]()